嘿,你有没有发现一个挺有意思的事儿?每次一聊到几何图形里的梯形,好多人就开始犯迷糊了,感觉好像这梯形星团的知识,别人都门儿清,就自个儿还在云里雾里呢!这不,就像平时考试,课本上好像没咋详细讲的那些梯形知识点,一到考试就冒出来考大家,好多人就懵圈啦!这到底是为啥呢?难道梯形的知识就这么难搞懂吗?
梯形知识只是小儿科,不用深究?
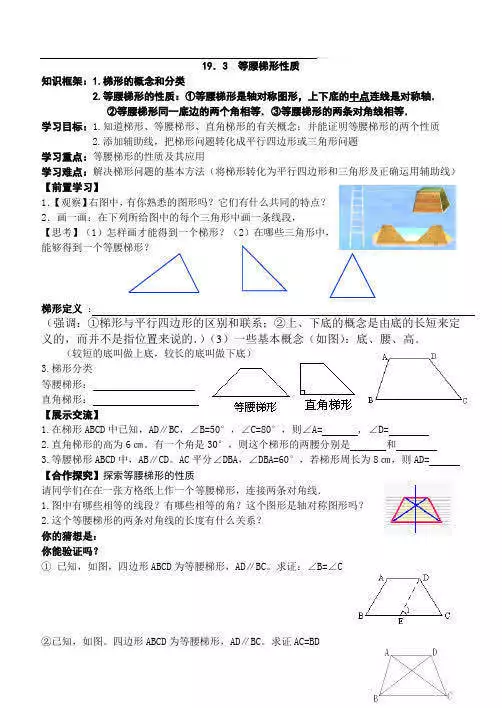
好多人觉得吧,梯形不就是那个有一组对边平行,另一组对边不平行的四边形嘛,看着挺简单的呀,能有啥高深的知识呢?可真这么想,那可就大错特错啦!就拿等腰梯形来说吧,它可不只是两腰相等那么简单哦。它同一个底上的两底角相等,不仅腰上的两组内角互补,两组对角也互补呢,这知识点够丰富吧?而且等腰梯形的两条对角线还等长,两对角线分割出的四个三角形,含腰的两三角形全等,含上底和下底的两三角形还是等腰三角形呢。这还没完,它还是轴对称图形,有一条对称轴,是过上下两底中点的直线,延长两腰还能得到一个等腰三角形呢。你说,这能是小儿科吗?要是不深究,到考试的时候,这些细节可就都抓瞎啦,那时候再后悔没好好学,可就晚咯。这难道还不能让你重视起梯形知识吗?
值得注意的是,还有特殊的直角梯形呀,有一个内角为90º的梯形就是直角梯形啦,在一些实际的几何应用场景里,它的特性也很关键呢。要是小瞧了这些特殊梯形的知识,那遇到相关题目可不就得干瞪眼啦?这能行吗?
梯形的高就那么一种理解方式?
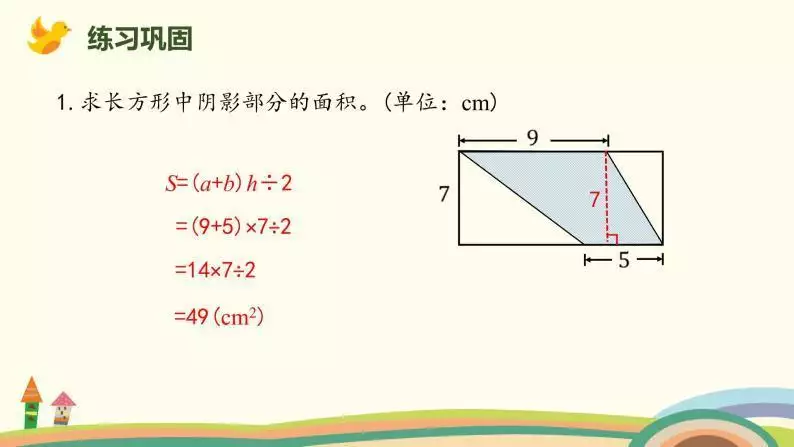
一提到梯形的高,可能不少人就觉得,不就是两底边之间的垂线段嘛,就这么简单呗。哼,那可不一定哦!梯形确实有无数条高,且都相等,这是没错啦。但你要是只停留在这个最基础的认识上,那可就有点浅啦。比如说在一些复杂的几何图形组合里,要准确找到梯形的高并且利用它来解题,那就得对高的概念有更透彻的理解呀。有时候,它可能和其他图形的边或者线段有着千丝万缕的关系呢,你要是没搞清楚,那解题思路可就全乱套啦。这时候你还能说梯形的高就那么简单,没啥可深挖的吗?
更关键的是,当我们在研究梯形的面积计算等问题的时候,对高的准确把握那可是相当重要的呀。要是连高都没搞明白,那面积算错了,后面的一系列计算不都跟着错啦?这可不像闹着玩的,你说是不是这个理儿呢?
梯形的中位线知识不重要?
梯形的中位线,就是两腰中点相连的线啦,有人觉得这玩意儿好像没啥大用似的。嘿,可别这么想呀!它平行于两底并且等于上下底和的一半呢,这可是个很重要的性质哦。在很多涉及到梯形的比例关系、相似图形等问题的解决中,中位线的知识那可都是关键因素呢。要是忽视了它,有些题目可能就卡在那儿解不出来啦。你想想,本来能轻松做出来的题,就因为没重视中位线知识,结果做不出来,多可惜呀!这难道还不能让你重新审视一下梯形中位线的重要性吗?
值得注意的是,在一些几何证明题里,巧妙运用梯形中位线的性质,往往能起到化繁为简的效果呢。要是把这么好用的知识给扔一边儿,那不是自己给自己找麻烦嘛。你还觉得它不重要吗?
所以呀,可别再觉得梯形知识没啥了不起啦,这里面的门道多着呢。大家可得好好把这些知识都琢磨透咯,别到时候别人都对梯形知识了如指掌,自个儿还在那懵懵懂懂的呀。下次再遇到梯形相关的问题,咱也能轻松应对啦,不是吗?
大家不妨回忆一下,自己以前在学习梯形知识的时候,有没有掉进过这些误区呢?欢迎在评论区分享哦。
#梯形知识 #几何误区 #学习心得

