编辑推荐
前几周我们一直在推出一些与生活或娱乐相关的数据分析文章,大家是不是都看得很开心呢?不过,本着劳逸结合的精神,本期有大量技术性、应用性极强的干货,也希望给大家带来一些启发……
介绍一种数据分析方法,大概总该从它的发展历史说起:K折交叉验证(K-fold CrossValidation)的思想来源于大名鼎鼎的统计学家Frederick Mosteller,哈佛大学统计学系的创始人。Mosteller博士的名字常出现在各类统计学书籍中,从面向普通读者的趣味介绍、到专业性极强的读物,这主要归功于他强大的创新精神,他希望将统计学思想应用在各种看起来风马牛不相及的领域里,并且还经常获得巨大的成功。
显然,上世纪五六十年代间,Mosteller博士的一大兴趣在于社会心理学。1954年,他发表论文、指出《金赛性学报告》中的统计学问题;两年后,他又针对数学心理学提出了Bush-Mosteller强化学习模型。而在1968年版的《社会心理学手册》中,Mosteller博士与著名数学家John Tukey合著了一篇日后影响深远的论文:"Data Analysis, Including Statistics". 论文的中心思想之一说起来很简单:为了验证模型对数据的拟合水平,应该将数据分成若干份,并将不同“份”的数据用于验证或预测。经过优化的拟合模型显然会比“真正的”模型更加贴合研究者手头的数据,因此,保留一部分数据用于模型验证,可以帮助研究者更好地对模型进行评价。
Mosteller博士撰写这篇文章主要是为了帮助手下的学生们,他们进行数据分析时常常面对样本量不足的困境;事实上,他提出的意见也的确大有帮助。近50年后,我们很容易视前人的思想为理所当然,但正是这篇文章启发了交叉验证的迅速发展。今天,我们就来以具体事例介绍一下K折交叉验证在金融银行领域的应用吧。
模型的验证技术分为外部验证和内部验证两种类型。顾名思义,外部验证是指我们把建立的模型应用于来自同一源(即具有相同的分布)的全新数据上,这将引起一个可信的预测误差的评价,不用说,它肯定是最严格的验证方法;然而,实际应用中的数据分析最常遇到的难题莫过于数据的缺乏,因此我们往往会被迫使用相同的数据来建立模型的评估模型。就这样,内部验证比外部验证更为普遍,而在内部验证技术中,最流行的是bootstrap和交叉验证。正如前文所述,交叉验证的诞生主要基于以下考虑:当我们用同一份数据来建立模型和估计预测误差时,通常会产生有偏的值,因为参数估计会为了反映给定数据集的特殊性而进行优化。
交叉验证的思想是把数据集分成两部分,第一部分用于构建模型,第二部分用于验证模型;并且,验证是一个反复进行的过程,最终将结果适当结合,用于随后的模型选择和评估。
显然,数据集如何划分是交叉验证的关键因素。根据区分的类型,我们有以下三种方法:
(1)留一份数据作为交叉验证集,通常简称为“留一验证(LOOCV)”;
(2)留多份数据作为交叉验证集;
(3)K折交叉验证。
方法1和2通常是近乎无偏的,但可能会有很高的方差,特别是对于小样本数据来说;而K折交叉验证则是在样本量不足、无法保证训练和验证两个数据集都具有足够的样本数据的情况下,用于验证模型稳定性的一种常用的方法,这种方法保证了所有数据都可以既用于训练模型也可以用于验证模型。
K折交叉验证的算法可以这样描述:初始数据采样分割成K个子样本,每次交叉验证中将某个子样本作为验证模型的数据,其他K-1个样本合集作为训练集;交叉验证重复K次,使得每个子样本验证一次,然后平均K次的结果或者使用其它结合方式,最终得到一个单一估测。这种方法的优势在于,同时重复运用随机产生的子样本进行训练和验证,每次的结果验证一次模型效果。
接下来,我们引入一桩实际案例,使用数据分析工作者的老朋友——SAS Enterprise Miner来进行更深入的学习和认知。
我们使用的数据来源于某信用卡公司的客户数据,共有6万多条记录,其中逾期客户占比为8.36%。数据分析的自变量中,有客户申请信用卡时填写的问卷(包括客户性别、年龄、户籍、婚姻、学历等人口统计属性)和客户在银行的交易行为数据(包括借款余额、使用信用卡频率等),所有数据已经进行了目录编码。我们的目标,是用26个自变量来拟合客户是否会逾期超过30天。通过SAS EM,我们利用如下两种交叉验证方法进行了Logistic模型构建和验证:
方法一:先拟合一个全样本模型,再把数据等分五份(即取k=5),分别标记为样本1、样本2、样本3、样本4和样本5。首先用样本1作为验证数据集、样本2到5作为训练数据集建立模型,然后用样本2作为验证数据集和样本1、3、4、5作为训练数据集建立模型……如此类推,最终我们会得到5个模型。最后我们来比较5个模型拟合统计量,检查他们是否稳定。
方法二:按照方法一建立5个子模型。检查5个子模型跑出来的自变量,把5个模型共有的自变量记录下来,最终使用这些共有的自变量来拟合全样本数据。
方法一得到的结果如何呢?我们来分析一下:
前期我们先利用数据分析的方法处理自变量缺失和数据偏倚等问题;然后,我们用全部样本拟合一个逐步回归模型,得到了对模型有贡献的自变量20个。反应模型效果的拟合统计量分别是:ROC索引=0.847,Gini系数=0.695,KS统计量=0.536。从这些评判指标可以看出全样本模型效果还是不错的。
接着再用5折交叉验证来拟合5个子模型:从训练数据和验证数据的ROC图可以看出,训练集和验证集的ROC图都比较靠向左上方,表示5个子模型效果都比较好,而且5条ROC曲线重合度非常高,说明5个子模型都很稳定;然后,我们来看模型比较得到的相关指标:5个子模型的ROC索引>0.8、Gini系数约为0.7,KS统计量>0.5,说明模型效果都很不错,子模型的相同统计量之间差别也很小,训练集和验证集的模型结果也基本差不多,这说明该模型效果较为稳定。基于以上,我们认为可以接受全样本模型的结果。
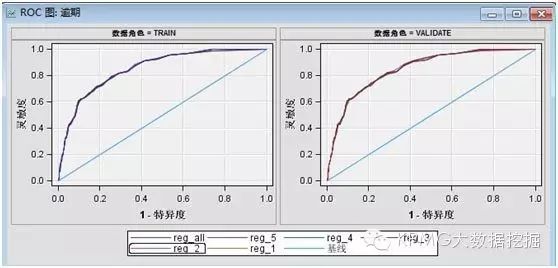

接下来,我们按照方法二进行K折验证:
由下图可以看出5个子模型的训练集和验证集的ROC曲线重合度较高,且都偏向于坐标左上方,ROC索引、Gini系数以及K-S统计量都较高,且各模型之间同一统计量的差别很小,说明模型效果较好,并且数据和模型都相对稳定。也就是说,我们可以利用5个子模型生产的若干交叉变量进行全样本模型的构建,本次模型结果中5个子模型都选择的变量有18个,然后就可以利用这些变量及全样本数据构建新的模型。
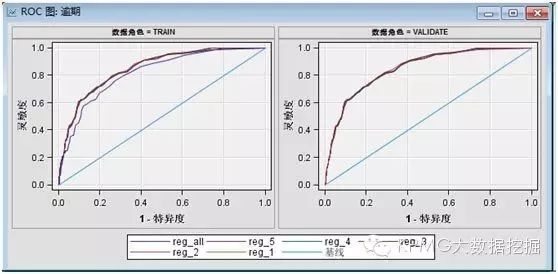

在用全量样本来拟合后,得到的统计量为:ROC索引=0.818,Gini系数=0.636,KS统计量=0.483。
比较而言,从以上的统计量来看,方法二的全样本模型的效果对比方法一的全样本模型效果有所下降,这是由于进入模型的自变量的减少而导致的,不过结果还是在可接收的范围内。综合来看,样本量不大时,为了提高模型稳定度,我们可以使用K折交叉验证方法,充分利用数据集对模型效果进行测试。但需要注意的是,这里的结论是在特定数据分布的情况下得出的,并不能作为经验法则。本次我们的样本数据分布较为理想、本身全样本模型就较为稳定,因此在应用中还需根据实际的数据情况作出取舍和与调整。
撰写这篇文章时,有位同学提醒我,今年正是Frederick Mosteller博士诞辰100周年。其实,每次想到“大数据分析”或者“文本挖掘”的话题,Mosteller博士都会出现在我的脑海里。大学时贝叶斯统计的第一节课上,教授讲述过一个“联邦党人文集作者案”的经典故事:《联邦党人文集》由85篇发表于18世纪80年代的文章组成,它们是研究美国宪法最重要的历史文献;然而,由于几位作者都使用了同一笔名,这85篇文章中始终有12篇的作者身份存在争议。在150余年的众说纷纭之后,Mosteller博士协同另一位统计学家David Wallance,使用统计学方法分析不同作者的写作风格,最终解决了这个问题。他们的研究结果发表在1962年的《时代周刊》上,不但震动了历史学研究者,更让统计学界大开眼界。
我们今天说起大数据,首先想起的一定是计算机中或者云端的的庞大数据集,然而在计算水平尚不发达的年代里,为了分析平均句长、或者"by"和"from"这样的虚词的使用倾向,Mosteller博士所拥有的“大数据”,是用打字机把《联邦党人文集》的全部文本打出来,然后人工剪出每个单词,并按照字母表的顺序、将它们分别汇集起来。
如前文所述,兴趣广泛的Mosteller博士自然也没有止步于文本挖掘。他曾分析1948年美国大选中杜威为何不敌杜鲁门;身为波士顿红袜队的球迷,他将数据分析引入棒球比赛的预测中;他分析过外科手术中麻醉药可能的危害,甚至研究过卡牌魔术与统计学的关系……Mosteller博士最令人惊叹之处,就是将数据分析的方法介绍到了旁人难以想象的广阔领域,——因为,归根结底,又有哪个领域不需要揭示表象背后的真相呢?
如今,昔日几百人亲手汇集的词库,已变成SAS取用的海量数据集;从前应用于心理学的验证算法,今天也可转用于金融领域之中。Mosteller博士说过:“有了统计学,说谎固然容易,但如果没有统计学,说谎只会变得更加容易。”而数据工作者的传承,始终在于对真相的追逐。
注:部分资料参见Frederick Mosteller博士的自传:The Pleasures of Statistics,推荐阅读。
关于我们我们是KPMG专业数据挖掘团队,在微信公众号中,我们会在每周六晚8点准时推送一篇原创文章。文章都是由项目经验丰富的博士以及资深顾问精心准备,内容也是结合实际业务的理论应用和心得体会等干货。欢迎大家关注我们的微信公众号,关注原创数据挖掘精品文章。如果想要联系我们,也可以在公众号中直接发送想说的话与我们联系交流。
长按二维码即可关注!也请随手推荐我们给你的小伙伴 ↓↓↓↓


