【调参侠的修炼笔记3】一文了解机器学习常见（超）参数

写在前面

【第一段可以跳过，都是废话】“一文读懂XXXXX”老标题党了，作为一个佛系撰写想法、没什么关注的研0菜狗，就是想看看“一文读懂”这个标题的威力（可以预想到也没什么威力）。这篇文章主要介绍了机器学习模型常见参数，不是像前两篇那样比较特别针对某一种模型的，当然了，不同的算法类别中的参数差别是很大的，这篇就是介绍一些典型参数的概念，毕竟自己目前还无法像大佬们一样所涉及的知识面那么广，不断成长嘛。

【这段可以简单一看】这篇文章主要解释了模型训练中神经网络的学习率，偏置，常见损失函数参数，支持向量机的C和sigma超参数、K最近邻的K等等，以及模型评估中的P，R，mAP等等。会按照样例和图表等方式进行说明，如果有理解的不对的地方也希望可以告知。

调参侠系列文章：

很酷不聊天：【调参侠的修炼笔记1】温度系数Temperature Parameter的讲人话解释100 赞同 · 10 评论文章

很酷不聊天：【调参侠的修炼笔记2】随机种子Seed的讲人话解释61 赞同 · 4 评论文章

Buqi：【调参侠的修炼笔记4】“熵”系列——信息量，熵，交叉熵，KL散度打包概念的讲人话解释8 赞同 · 0 评论文章

基本概念

首先，需要明确参数和超参数的概念：

1 神经网络

下面主要通过列举的方式来梳理不同类型算法/模型中的常见（超）参数

1.1 学习率 η\eta

η\eta 决定了（监督学习&深度学习的）目标函数能否收敛到局部最小值以及何时收敛到最小值。

如下图所示，学习率可以理解为步幅。过小时，收敛过程将十分缓慢；过大，梯度可能会在最小值附近来回震荡，甚至可能无法收敛。

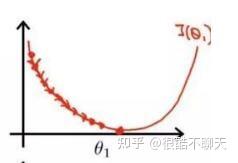
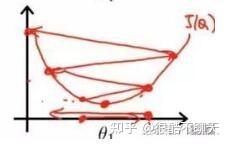
另外，如下图所示，固定学习率时，当到达收敛状态时，结果会在最优值附近一个较大的区域内摆动；而当随着迭代轮次的增加而减小学习率，收敛时结果将在最优值附近一个更小的区域内摆动。（之所以曲线震荡朝向最优值收敛，是因为在每一个mini-batch中都存在噪音）。

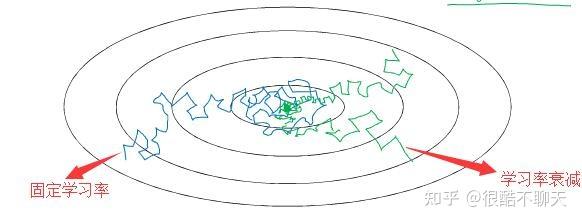
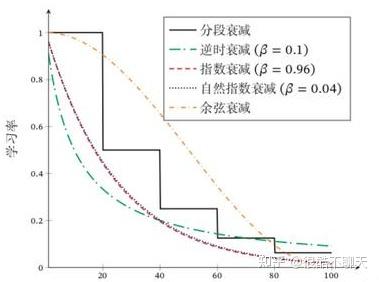
1、离散下降

大多初始设置一个较大的学习率（如0.01），然后随着迭代次数的增加，减小学习率（常规设置为每轮训练学习率减半）。

2、指数衰减

学习率按训练轮数增长指数差值递减。例如： α=0.95epoch_num⋅α0\alpha=0.95^{epoch\_num} \cdot \alpha_{0} ，以及 α=kepoch_num \alpha = \frac{k}{\sqrt {epoch\_num}} ，其中 kk 为新引入的超参数，epoch_num为当前epoch的迭代轮数。

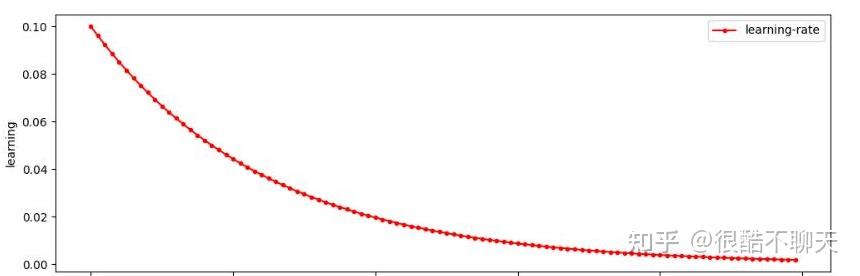
3、分段衰减

学习率按照公式 α=α1+decayrate∗epochnum\alpha = \frac{\alpha}{1+ {decay _ rate} * {epoch _ num}} 变化， decay_rate控制减缓幅度。

4、余弦退火衰减

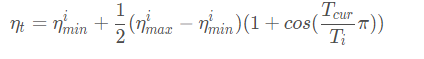
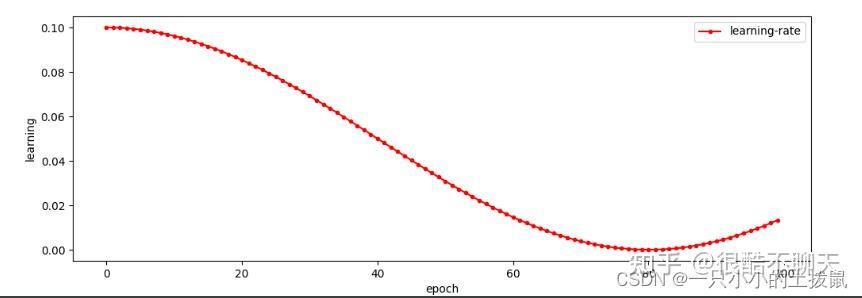
按照周期变化，其包含的参数和余弦知识一样，参数T_max表示余弦周期；eta_min表示学习率的最小值，默认它是0表示学习率至少为正值。确定一个余弦函数需要知道最值和周期，其中周期就是T_max，最值是初始学习率。

1.2 正则化参数 λ\lambda

正则化项的引入，主要为了解决过拟合问题，增强模型泛化能力。如下图所示，分别表示了欠拟合，拟合，过拟合的三种回归的结果。

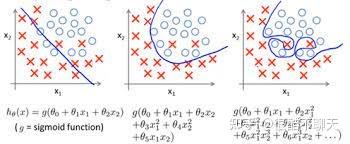
说白了，过拟合就是通过过量的参数，来对数据进行解释，或者说对数据分布的规律进行表征。这种情况下，模型就只能够对当前的数据进行很好的表征，如果增加一个样本，甚至是一百个，一万个，根据概率，这样的曲线很难对新的数据分布进行表示。为了消除这种影响，正则化的概念就被引入到回归与分类任务当中。通过保留所有的变量，降低一些不重要的特征的权值，使得特征的参数矩阵变得稀疏，进而使每一个变量都对预测产生适当的影响。

如图所示：

原始的损失函数只有前面那一部分，也就是说当前面那部分的数值越小，就证明模型拟合的越成功，但是这种情况下存在过拟合的问题。因此，后面的正则项其实是引入了参数的惩罚项，说白了，就是产生的参数越多，那么后面的正则化项的值就越大，该模型拟合的损失就越大，从而来控制模型拟合的程度。

常见的正则化包括 L1L_{1} 正则， L2L_{2} 正则，相关的具体理解，可以看这篇博客：

1.3 神经网络结构

（层数，神经元个数，dropout等）

关于神经网络实际上是一个大的话题，因为涉及到的参数太多，那么从结构角度来讲，我们可以简单概括为网络层数，每层神经元个数，神经元之间通道数。因为已知这三点，我们可以大致绘制出这个网络的结构，如下图所示：

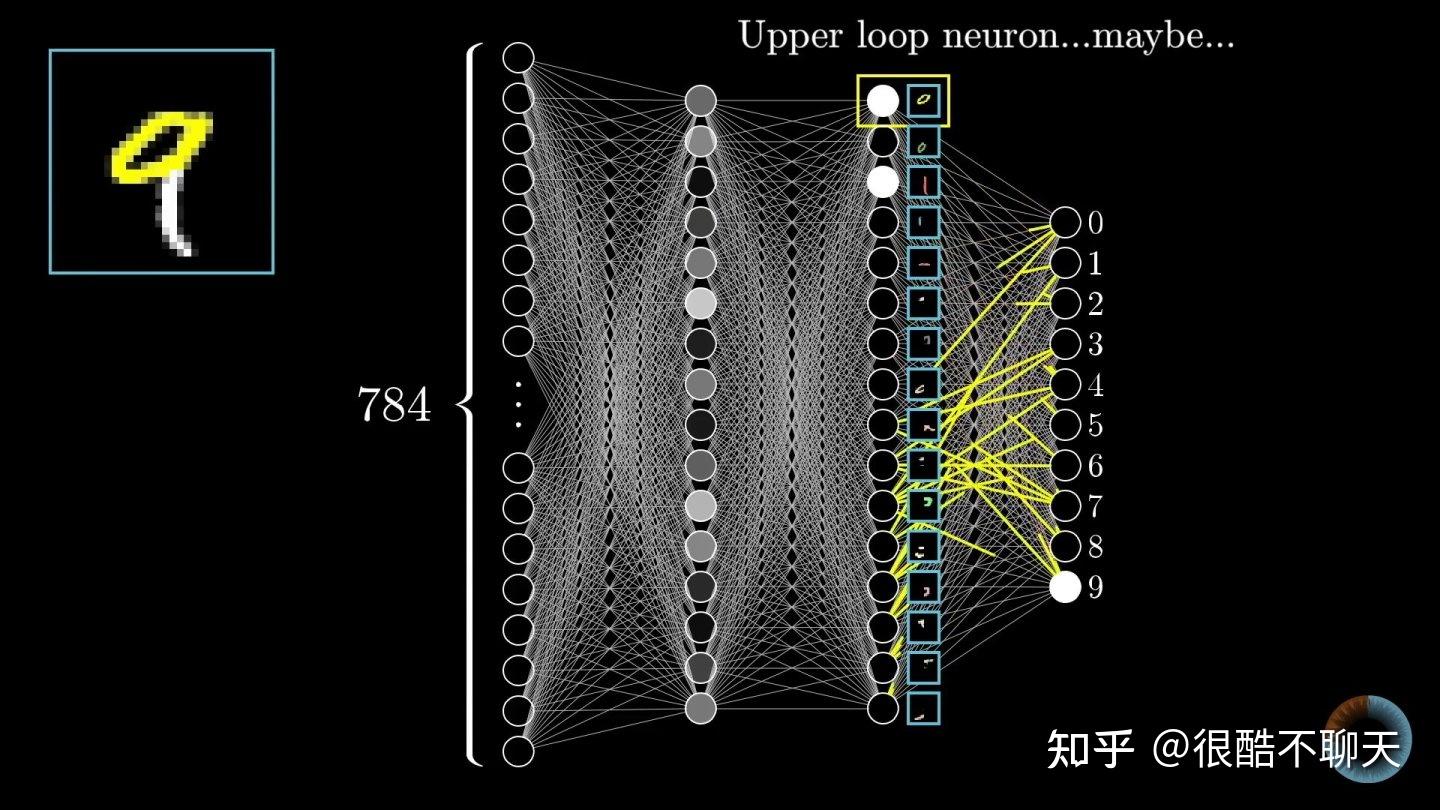
说白了，神经网络就像是一个拟合器，根据学习的数据拟合这种数据的分布规律，构建模型，从而应对并高效解决相似问题。那么这种拟合的过程是通过不同层间神经元传递而实现的，就像人脑信号传递的过程。

假设我们需要识别小狗这种动物，首先我们将数据输入到网络中，每个神经元把最初的输入值按照初始化结果乘以相应的权重，层层传递后，最后算出一个总和（类别），然后根据该类别与输入数据所包含标签“小狗”进行对比，根据偏差反向对神经元之间的权重进行调整，最终可以根据该数据获得拟合后的小狗判别器。

当下次进行检验时，将数据输入获得的模型中，便可以输出是否为“小狗”的结果，从而实现“判别小狗”的目标。也称为“反向传播”。

对于最简单的神经网络而言，其参数并不需要调整，直接通过前向传播预测即可。该过程可以表示为：

说白了，神经网络包含三步：

即使用权重中的知识解释输入数据的信息。

另一种理解神经网络权重的方法是将权重作为网络的输入和预测之间敏感度的度量：如果权重非常高，即使是最小的输入也可以对预测结果产生非常大的影响；如果权重很小，那就算是很大的输入也只能对预测结果产生很小的扰动。

我们既然清楚了神经网络的工作原理，那么如何确定神经元层数以及每层个数呢？

神经网络是由输入层，隐藏层和输出层组成的，输入层和输出层自然不必多说，我们需要确定隐藏层的层数。而隐藏层包含卷积层（Convolution），激活层（Activation），池化层（Pooling），以及全连接层（Fully connected），简单来讲：卷积层+激活层（卷积层通过不断采样，模糊后可以过滤掉不重要的特征，激活层可以根据目标锁定卷积过滤后的数据中的各个特征，比如水果的边缘，颜色等等），池化层通过下采样，可将卷积层所产生的大量数据，全部缩小成更通用和可消化的形式，从而大大缓解了计算压力。这三个网络层通常按照卷积层—激活层—池化层的顺序进行连接：

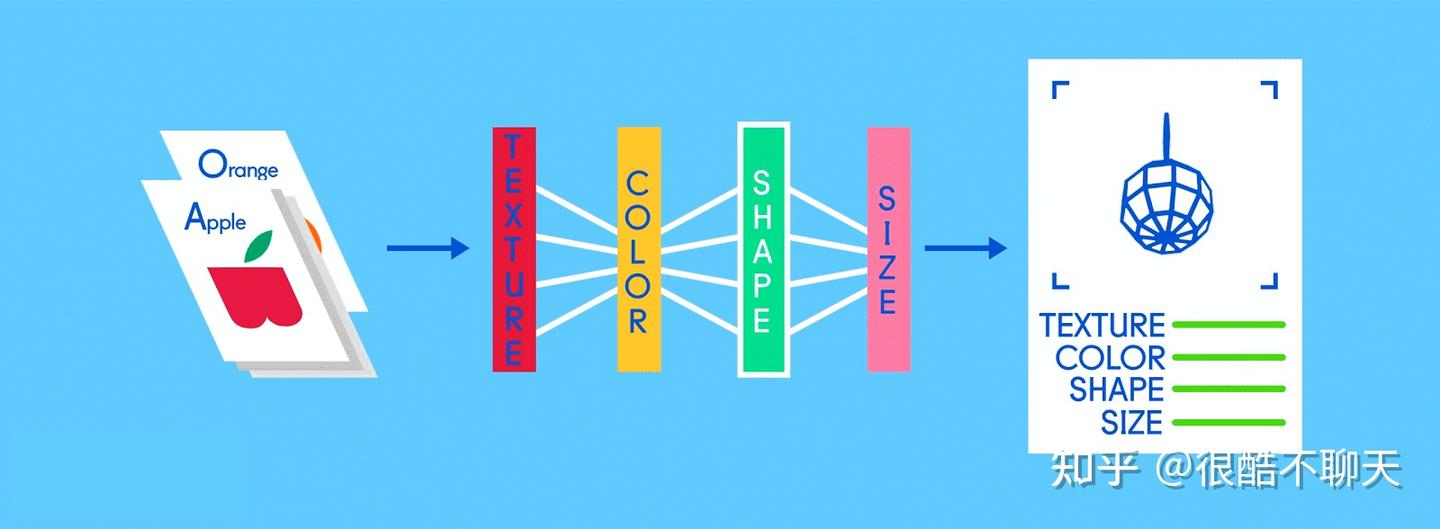
全连接层则是将每个削减的或“池化的”特征图“完全连接”到表征了神经网络正在学习识别的事物的输出节点（神经元）上。一个神经网络的隐藏层通常也按照：n*卷积-激活-池化层+1*全连接层的方式构建网络结构。

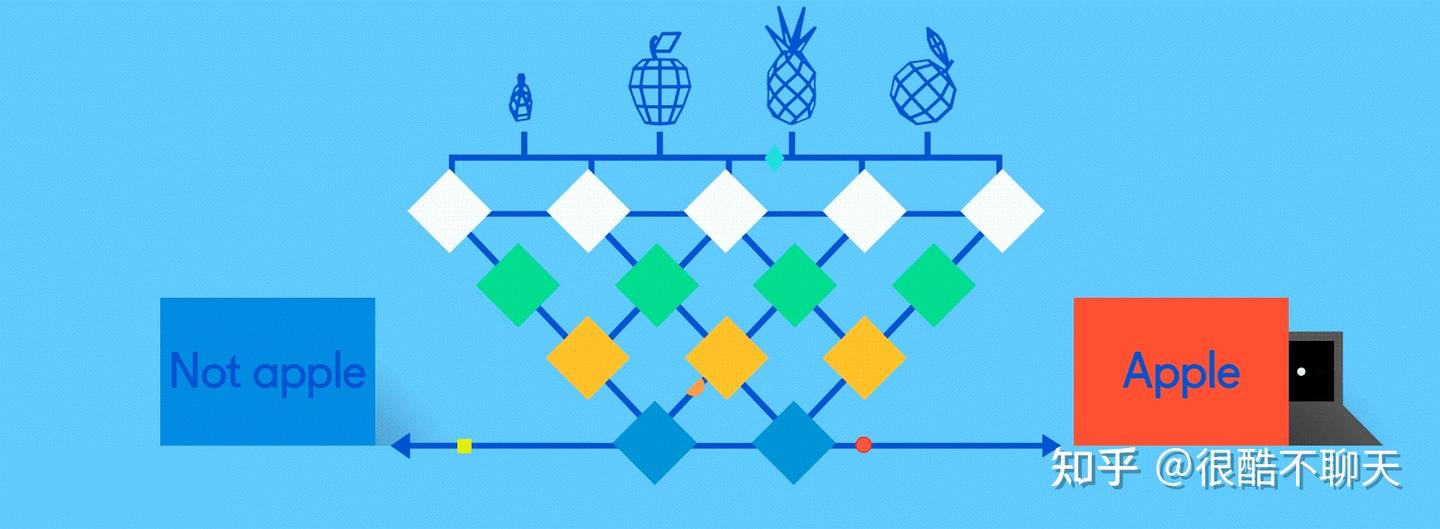
那么这个“n*卷积-激活-池化层+1*全连接层”中的N如何选取呢。对于一些很简单的数据集，一层甚至两层隐藏元都已经够了，隐藏层的层数不一定设置的越好，过多的隐藏层可能会导致数据过拟合。对于自然语言处理以及CV领域，则建议增加网络层数，比如说近些年特别火的深度学习，实际上就是加深网络层数，从而处理更加细节的特征，在多个视觉任务上获得了优越的效果。

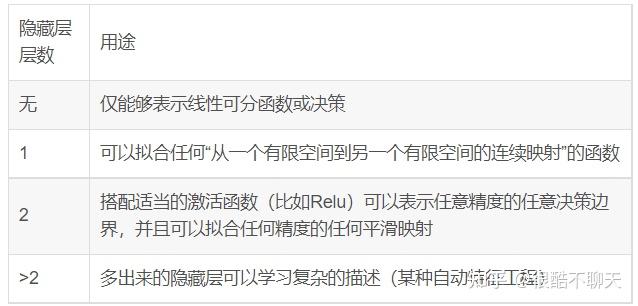
我们可以按照这样的原则去构建网络结构：

实际上，我们需要明确这样的结论：层数越深，理论上来说模型拟合函数的能力增强，效果会更好（针对数据较为复杂的情况），但是实际上更深的层数可能会带来过拟合的问题，同时也会增加训练难度，使模型难以收敛。

而对于神经元个数而言，说实话其影响远不及神经网络层数对模型性能的影响。如果说非要进行设计的话，我了解到的是如下的三个原则（因为自己目前也没有很多创新，只是按照前辈们的总结进行学习）：

说白了，一个模型的设计建议就是：从一个较小数值比如1到3层和1到100个神经元开始不断试验来进行微调，如果欠拟合就慢慢添加更多的层和神经元，如果过拟合就减小层数和神经元。

代码如下

单输入单输出：

多输入单输出：

单输入多输出：

多输入多输出：

1.4 batchsize

batchsize是一个非常简单的指标，即训练过程中每批数据量的大小。深度学习通常用SGD（随机梯度下降）的优化算法进行训练，一次迭代（1 个iteration）训练batchsize个样本，计算它们的平均损失函数值，来更新参数。合适的batch size范围主要和收敛速度、随机梯度噪音有关。

当然，对于这个计算过程，计算梯度所需的样本数量太小会导致效率低下，无法收敛。太大会导致内存撑不住。因此，当Batch Size增大到一定程度后，其下降方向变化很小了。

简单来讲，batchsize就是考虑到有时候数据量可能很大，不能全部将数据送入到内存中，每次选 n 条样本送入内存，这个 n 就是batchsize。

batchsize的设置可以看这篇博客：

在模型的超参数设计的过程中，batch size可以说是所有超参数里最好调的一个，也是应该最早确定下来的超参数。因此很多人选择先选好batch size，再调其他的超参数。

常见的batch size值为从2到32之间的数值，LeCun曾经就在论文中提到了关于该参数的设置问题：

Training with large minibatches is bad for your health. More importantly, its bad for your test error. Friends don‘t let friends use minibatches larger than 32. Lets face it: the only people have switched to minibatch sizes larger than one since 2012 is because GPUs are inefficient for batch sizes smaller than 32. Thats a terrible reason. It just means our hardware sucks.

所以说，好的实验表现都是在batch size处于2~32之间得到的，常见的batchsize数值包括32，16，8等，而这些数值都是根据setting的大小进行选取的（比如setting（～100 epochs），batch size一般不会低于16）。

1.5 Epoch-学习的回合数

简单来讲，一个epoch指的就是用训练集中的全部样本训练一次，即所有的数据送入网络中， 完成了一次前向计算+反向传播的过程。下面的例子展示了这个参数的具体意义：

1.8 代价函数

代价函数 J(\theta) ，也称为损失函数，loss function，是用于判断模型预测值和真实值之间的差距的指标。而我们的模型训练就是优化代价函数的过程（即求得最优 \theta 的过程），代价函数对每个参数的偏导数就是梯度下降中提到的梯度，防止过拟和时添加的正则化项也是加在代价函数后面的。

代价函数的设置需要满足两个最基本的要求：

对于回归问题，最基本的就是线性回归和逻辑回归，其中线性回归通常采用均方误差：

J(\theta_{0},\theta_{1})=\frac{1}{2m}\sum_{i=1}^{m}(\hat{y}^{i}-y^{(i)} )^{2}

逻辑回归通常采用交叉熵（Cross Entropy）损失：

J(\theta)=-\frac{1}{m}\left [ y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)})) \right ]

而对于多分类问题，则通常使用比如softmax函数等作为代价函数。

关于代价函数的相关知识点，可以参考如下文章：

1.9 权重初始化

对于神经网络的训练来讲，初始化是十分重要的。举一个比较极端的例子，如果把神经网络的权重或者参数都初始化为 0，那么梯度下降将不会起作用。

1.10 神经元激活函数

在神经网络相关模型与算法中，我们经常会听到“激活函数”这个名词时，在很多论文的experimental setup中会提到相关的设定，比如常见的sigmoid, Relu等等。在1.3中我们知道神经网络的计算是通过神经元之间的数值传递与变换等来实现最终的计算的，了解到这个流程，我们不难理解，如果不添加激活函数，也就是说在传递的时候只是利用权值进行加乘，那么就会变成权重与偏差间的线性变换，即使是多层网络，也会是线性变换的组合，所以只能完成线性回归的任务。

基于此背景，如果我们希望模型可以处理复杂任务，只能希望能够有别的方式来赋予模型其他的任务。因此，使用激活函数对输入进行非线性变换就成为了一种很好的方案，使神经网络能够学习和执行更复杂的任务。

1.11 数据规模

对于神经网络中，特别是有监督学习，需要数据作为支撑来进行模型的训练。我们可以简单理解就是数据规模就相当于人类学习的知识量，模型本身就好比大脑，我们希望机器可以学会更多的知识，从而进行更加准确快速的判断，因此，我们就需要喂给它更大规模的数据，而随着算法的迭代，后来人们学会了从已经初步开发的模型（已经具有一定基础的大脑）开始进行新的学习，完成新的任务，所以数据规模以及标签量也在逐渐从大规模转向无标签，当然，这些就属于自监督或者无监督等领域的范畴了，这里就不过多赘述。

另外，除了模型的发展伴随着对不同数据规模的需求，模型本身也会一定程度上收到数据的影响。就拿常见的欠拟合，过拟合来讲，大规模的数据对应简单的模型，很容易出现欠拟合的问题，而小批量数据使用复杂的模型进行拟合，则很容易出现过拟合的问题。（或许有些笼统，但是数据与模型这两者之间是有着不可分割的关系的）。

早期的时候，类似imagenet等数据集的出现是很大程度上推动了CS的发展的，近些年人们也在寻找数据规模与模型参数（大模型）的边界。

2 决策树

决策树是一种机器学习的方法，通常用于解决分类问题，常见的生成算法有ID3, C4.5和C5.0等。决策树是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。如下图所示。

我们将数据依次按照属性进行树形结构的设计，然后通过剪枝等操作进行进一步的修饰，并根据所构建的树进行进一步的判断与预测。

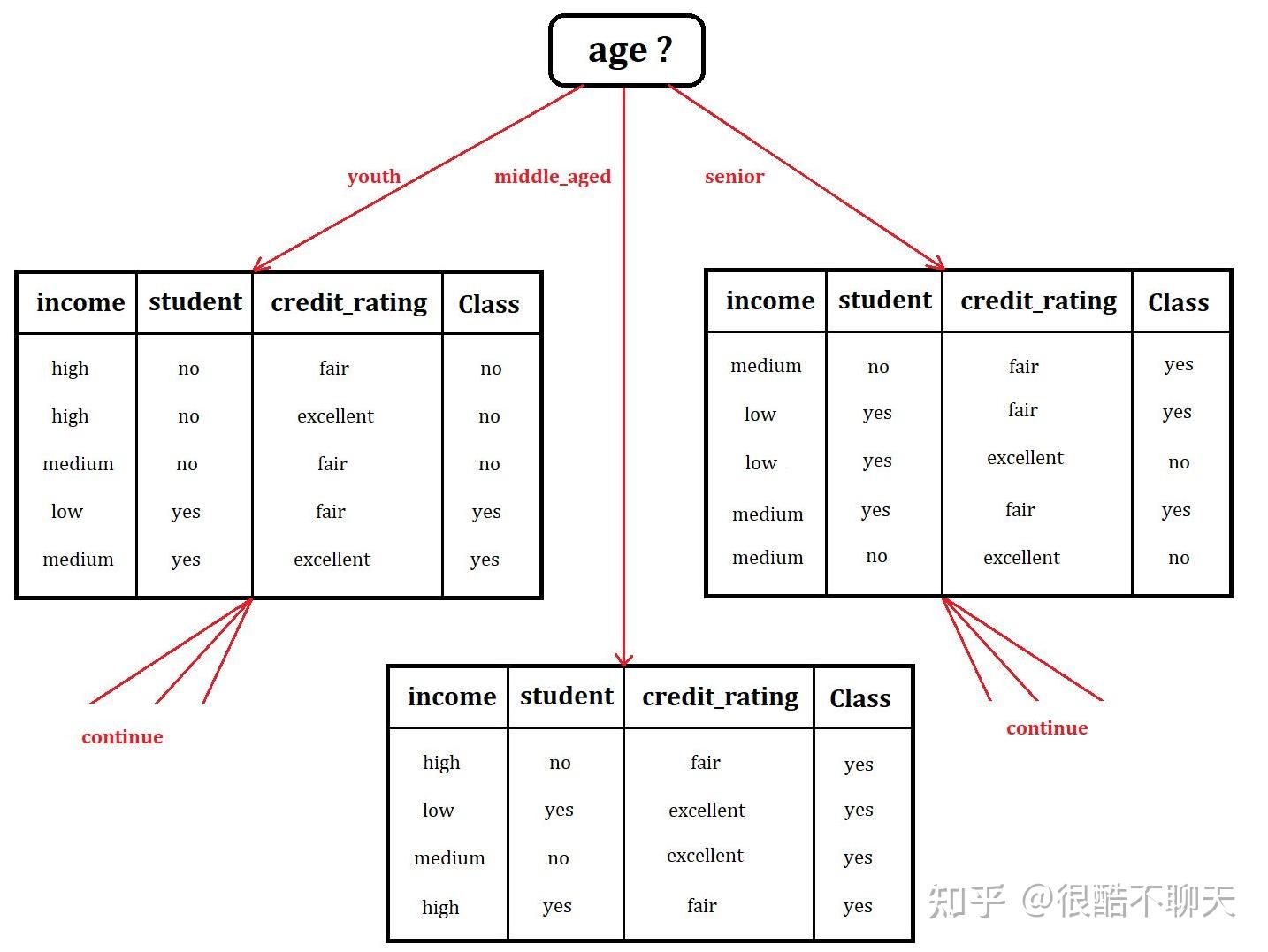
3 随机森林

4 支持向量机

5 K近邻

6朴素贝叶斯

【2022.8.15记，保持每日更新】