
长短期记忆网络(Long Short-Term Memory,LSTM)是一种特殊的循环神经网络(RNN),主要用于处理和预测序列数据,在自然语言处理、语音识别、时间序列预测等领域有广泛应用。
时序数据处理
对于回归问题,一个样本对应的是一个输出值;对于分类问题来说,可能多个样本对应同一个分类标签;对于时序数据问题来说,可以看出是一个列向量,例如股票价格预测,我们希望从以往时间的数据来预测后面的数据。
因此,对于LSTM模型时序预测问题的建模关键是对预测的一维时序数据的处理。
有关如何根据时序数据构造LSTM模型训练集和测试集的输入数据和输出数据的例子参考:
搞清楚时序数据转换成矩阵的操作之后,基于LSTM的时序预测问题就不难理解了。
MATLAB实现代码
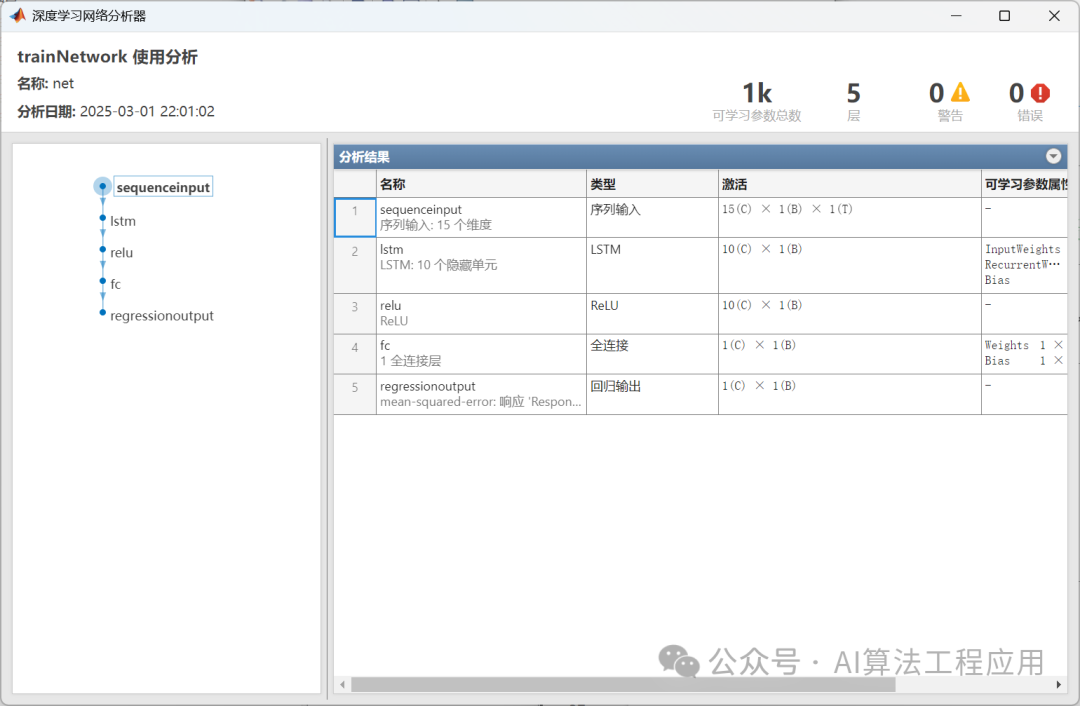
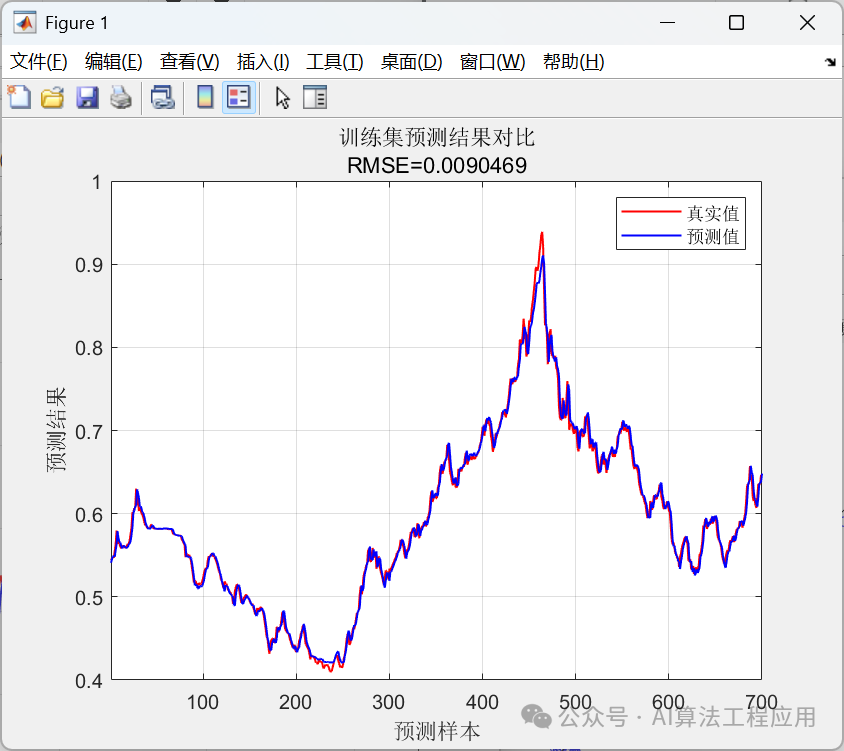
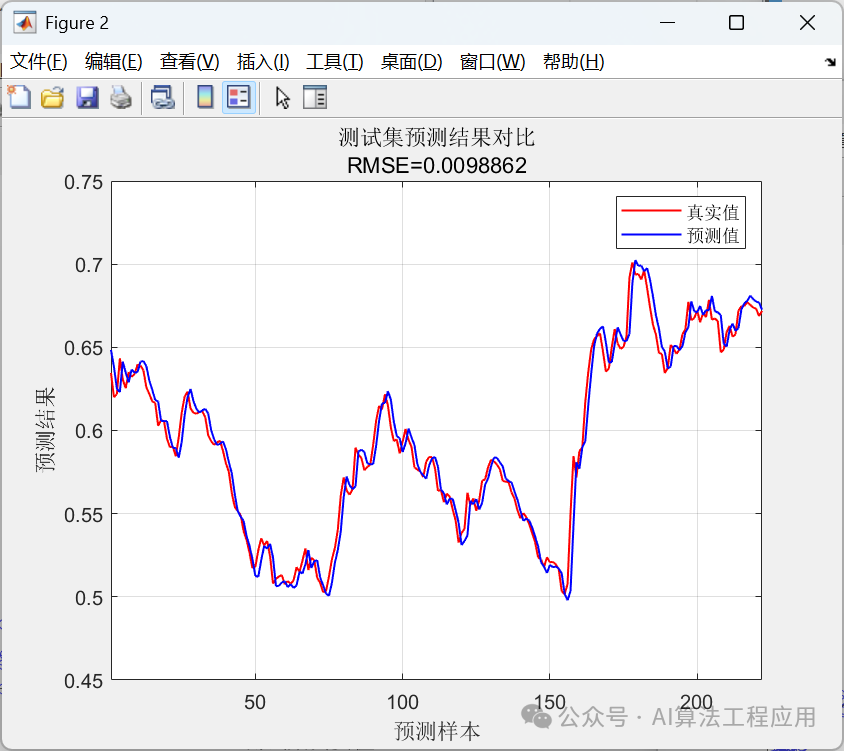
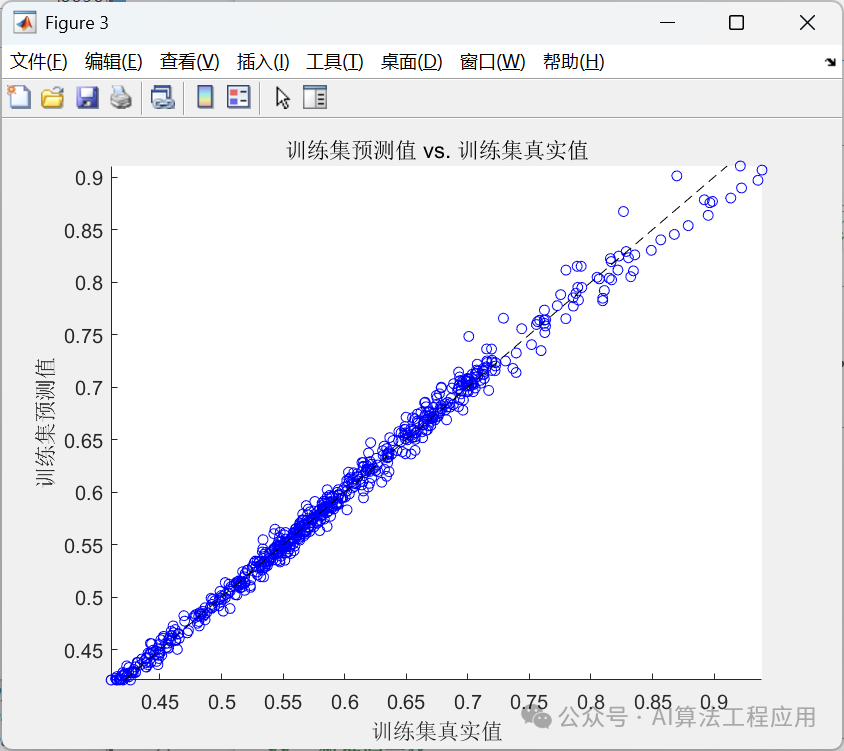
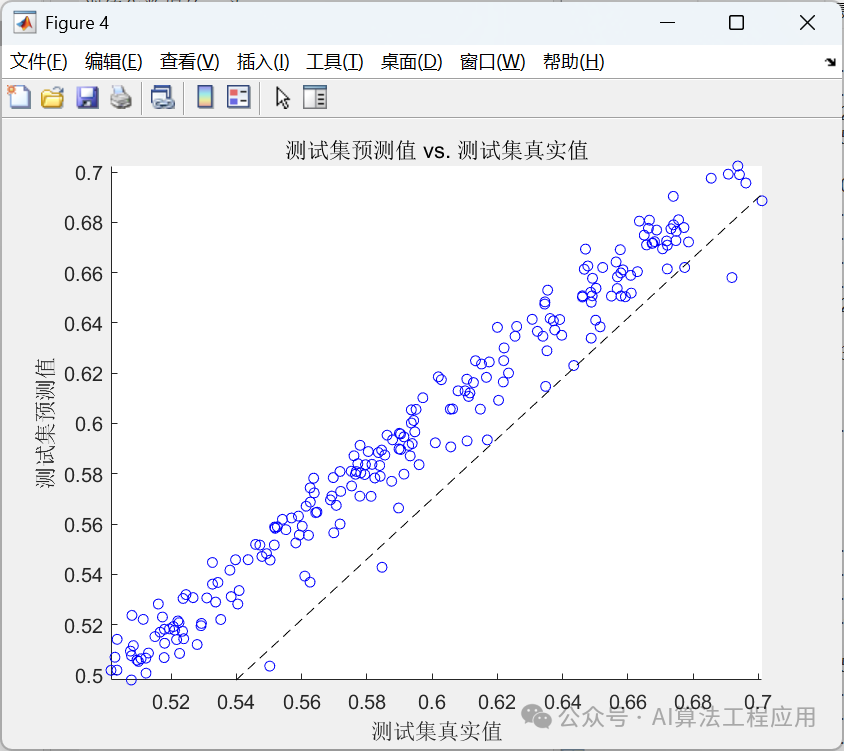
%% 清空环境变量clear % 清空变量clc % 清空命令行warning off % 关闭报警信息close all % 关闭开启的图窗%% 导入数据(时间序列的单列数据)result = xlsread(数据集.xlsx);%% 数据分析num_samples = length(result); % 样本个数 kim = 15; % 延时步长(kim个历史数据作为自变量)zim = 1; % 跨zim个时间点进行预测%% 划分数据集for i = 1: num_samples - kim - zim + 1 res(i, :) = [reshape(result(i: i + kim - 1), 1, kim), result(i + kim + zim - 1)];end%% 划分训练集和测试集temp = 1: 1: 922;P_train = res(temp(1: 700), 1: 15);T_train = res(temp(1: 700), 16);M = size(P_train, 2);P_test = res(temp(701: end), 1: 15);T_test = res(temp(701: end), 16);N = size(P_test, 2);%% 数据归一化[P_train, ps_input] = mapminmax(P_train, 0, 1);P_test = mapminmax(apply, P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);t_test = mapminmax(apply, T_test, ps_output);%% 数据平铺% 将数据平铺成1维数据只是一种处理方式% 也可以平铺成2维数据,以及3维数据,需要修改对应模型结构% 但是应该始终和输入层数据结构保持一致P_train = double(reshape(P_train, 15, 1, 1, M));P_test = double(reshape(P_test , 15, 1, 1, N));t_train = t_train;t_test = t_test ;%% 数据格式转换for i = 1 : M p_train{i, 1} = P_train(:, :, 1, i);endfor i = 1 : N p_test{i, 1} = P_test( :, :, 1, i);end%% 创建模型layers = [ sequenceInputLayer(15) % 建立输入层 lstmLayer(10, OutputMode, last) % LSTM层 reluLayer % Relu激活层 fullyConnectedLayer(1) % 全连接层 regressionLayer]; % 回归层%% 参数设置options = trainingOptions(adam, ... % Adam 梯度下降算法MaxEpochs, 1200, ... % 最大训练次数InitialLearnRate, 5e-3, ... % 初始学习率LearnRateSchedule, piecewise, ... % 学习率下降LearnRateDropFactor, 0.1, ... % 学习率下降因子LearnRateDropPeriod, 800, ... % 经过 800 次训练后 学习率为 0.005 * 0.1Shuffle, every-epoch, ... % 每次训练打乱数据集Plots, training-progress, ... % 画出曲线Verbose, false);%% 训练模型net = trainNetwork(p_train, t_train, layers, options);%% 仿真预测t_sim1 = predict(net, p_train);t_sim2 = predict(net, p_test );%% 数据反归一化T_sim1 = mapminmax(reverse, t_sim1, ps_output);T_sim2 = mapminmax(reverse, t_sim2, ps_output);%% 均方根误差error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);%% 查看网络结构analyzeNetwork(net)%% 绘图figureplot(1: M, T_train, r-, 1: M, T_sim1, b-, LineWidth, 1)legend(真实值, 预测值)xlabel(预测样本)ylabel(预测结果)string = {训练集预测结果对比; [RMSE= num2str(error1)]};title(string)xlim([1, M])gridfigureplot(1: N, T_test, r-, 1: N, T_sim2, b-, LineWidth, 1)legend(真实值, 预测值)xlabel(预测样本)ylabel(预测结果)string = {测试集预测结果对比; [RMSE= num2str(error2)]};title(string)xlim([1, N])grid%% 相关指标计算% R2R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;R2 = 1 - norm(T_test - T_sim2)^2 / norm(T_test - mean(T_test ))^2;disp([训练集数据的R2为:, num2str(R1)])disp([测试集数据的R2为:, num2str(R2)])% MAEmae1 = sum(abs(T_sim1 - T_train)) ./ M ;mae2 = sum(abs(T_sim2 - T_test )) ./ N ;disp([训练集数据的MAE为:, num2str(mae1)])disp([测试集数据的MAE为:, num2str(mae2)])% MBEmbe1 = sum(T_sim1 - T_train) ./ M ;mbe2 = sum(T_sim2 - T_test ) ./ N ;disp([训练集数据的MBE为:, num2str(mbe1)])disp([测试集数据的MBE为:, num2str(mbe2)])%% 绘制散点图sz = 25;c = b;figurescatter(T_train, T_sim1, sz, c)hold onplot(xlim, ylim, --k)xlabel(训练集真实值);ylabel(训练集预测值);xlim([min(T_train) max(T_train)])ylim([min(T_sim1) max(T_sim1)])title(训练集预测值 vs. 训练集真实值)figurescatter(T_test, T_sim2, sz, c)hold onplot(xlim, ylim, --k)xlabel(测试集真实值);ylabel(测试集预测值);xlim([min(T_test) max(T_test)])ylim([min(T_sim2) max(T_sim2)])title(测试集预测值 vs. 测试集真实值)结果展示
训练集数据的R2为:0.99247测试集数据的R2为:0.9666训练集数据的MAE为:0.0062985测试集数据的MAE为:0.007317训练集数据的MBE为:0.00032334测试集数据的MBE为:0.00034658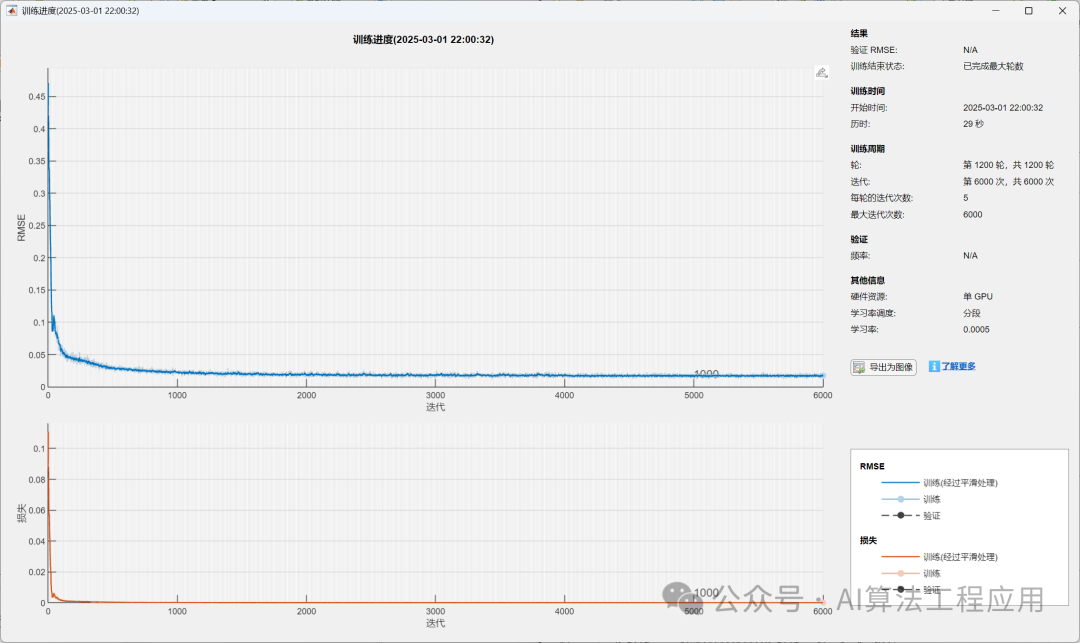
往期回顾
回归预测问题:
01. 机器学习模型 | BP神经网络原理及MATLAB回归实现
02. 机器学习模型 | 径向基函数神经网络(RBFNN)原理及MATLAB回归实现
03. 机器学习模型 | 随机森林(Random Forest)原理及MATLAB回归实现
04. 机器学习模型 | 长短期记忆网络(Long Short-Term Memory,LSTM)原理及MATLAB回归实现
分类预测问题:
01. 机器学习模型 | BP神经网络MATLAB分类预测实现
02. 机器学习模型 | 径向基函数神经网络(RBFNN)MATLAB分类预测实现
03. 机器学习模型 | 随机森林(Random Forest)MATLAB分类预测实现
04. 机器学习模型 | 长短期记忆网络(Long Short-Term Memory,LSTM)MATLAB分类预测实现
时序预测问题:
01. 机器学习模型 | BP神经网络MATLAB时序预测实现
