引言:
地心运动等非线性因素的存在使得建立和维持具有1毫米精度大地测量基准框架成为国际大地测量学界面临的重要挑战。精确测定特定时刻的地心运动坐标不仅是实现毫米级大地基准框架的关键任务之一,还为地球质量分布的物理解释以及地球动力学研究提供了重要的科学依据。因此深入研究地心运动机制及其精确测定方法,对于提升大地测量精度和深化地球系统科学研究具有重要的理论意义和应用价值。
GNSS直接估计地心运动参数结果与分析
本文采用地心运动直接估计方法中的参数估计法,基于GNSS观测数据解算了2021年至2023年的地心运动时间序列。太阳光压力(Solar Radiation Pressure, SRP)是影响地心运动参数估计精度的关键因素之一,因此研究了北斗三号系统(BDS-3)在不同SRP模型配置下的地心运动解算结果,探讨了同步估计地心运动参数时对精密定轨的影响。BDS-3作为中国独立建成的新一代全球卫星导航系统,其独特的星座构型与信号特性可能对地心运动的估计提出新的挑战,而目前鲜有学者针对SRP对BDS-3解算地心运动的影响开展深入研究,可为优化BDS-3在地心运动解算中的应用提供了新的参考。
1数据与策略
1.1 实验数据
根据中国测绘科学研究院-北斗分析中心多年的运行经验总结出的观测较为稳定的全球测站列表,同时考虑到地心运动解算过程中测站分布需尽可能均匀,在MGEX网络中选取了170+测站参与解算,测站分布如图所示。
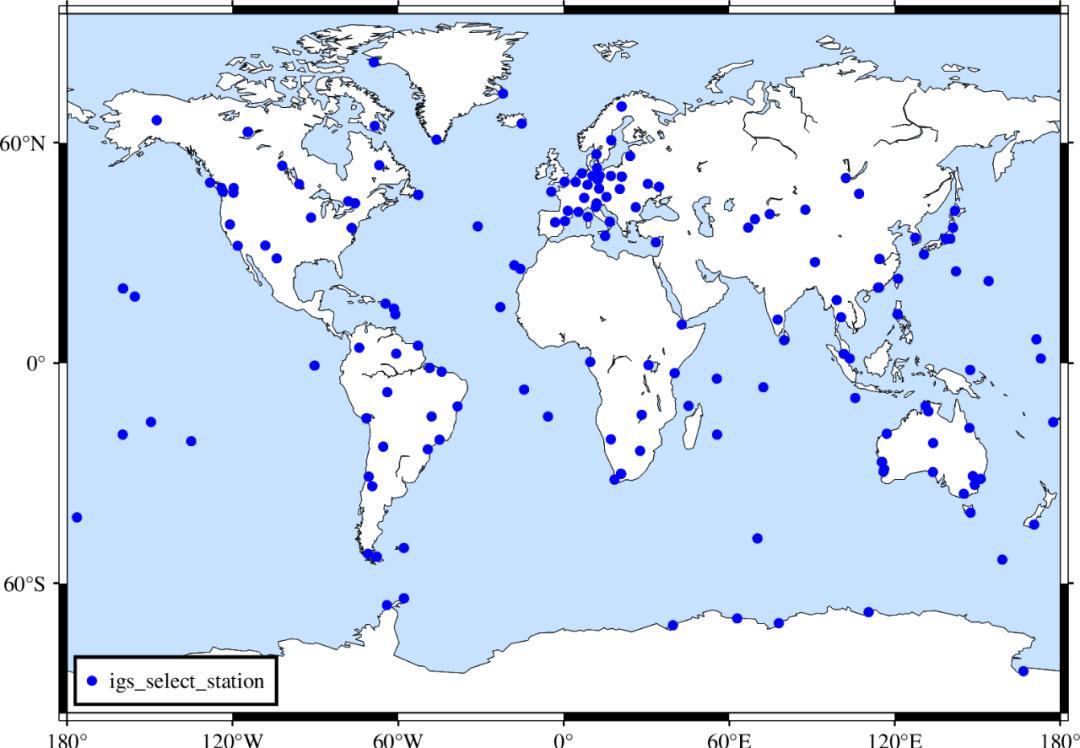
图1 选取测站分布图
1.2 解算策略
实验解算过程中具体策略见表1。测站选取了MGEX网络中相对稳定、均匀的170测站,采用了2021.01.01~2023.12.31观测数据(3年数据足以可靠地估计线性项、年度项及交点年误差),对BDS-3系统采用B1/B3进行双频非差无电离层组合解算地心运动。已有研究表明,采用三天观测弧长进行地心运动观测优于一天观测弧长,所以本实验采用72 h观测弧长,观测值采样率设置为300 s。采用TURBOEDIT模型对观测数据进行质量控制,包括粗差探测及周跳探测等。最低截止高度角设置为15°并且依据高度角对观测值进行定权。不同系统的全球导航卫星系统轨道高度均在20000 km以上,在此高度受地球重力场的影响较小,使用EGM2008模型12阶即可。N体引力采用DE405模型进行改正;同时估计固体潮及海潮,相对论相应使用IERS2010模型进行改正。根据无电离层组合观测公式,待估参数包括测站坐标、卫星初始状态、接收机钟差、卫星钟差、模糊度参数、对流层延迟及地心运动。其中测站坐标强约束到IGS SINEX产品中,卫星初始状态每一弧段约束到CODE精密星历产品,接收机与卫星钟差进行白噪声估计,进行双差模糊度固定,对流层使用Saastamoinen模型与GMF投影函数进行改正,在框架转换过程中求解地球自转参数,依据参数估计法估计地心运动且地心运动三方向参数约束设置为0.1 m。
表1 参数估计法解算地心运动策略表

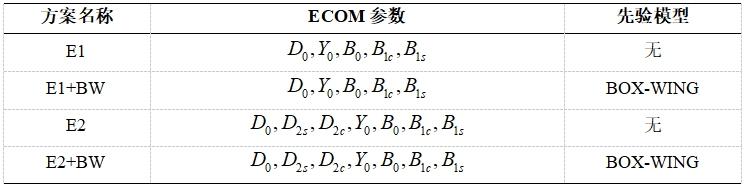
表2总结了本实验关于太阳光压模型测试用例的命名规则,选择了基于ECOM模型的不同变体同时考虑到是否引入BW先验模型两种情况,分别对不同系统进行不同参数设置进行实验。
表2 有关SRP的不同解决方案的描述
2BDS-3解算地心运动时序与分析
BDS-3系统是全球首个多星座全球导航卫星系统,截至目前由30颗卫星组成,分别是24颗中圆地球轨道(Medium Earth Orbit,MEO)卫星、3颗倾斜地球同步轨道(Inclined Geosynchronous Orbit,IGSO)卫星以及3颗地球静止轨道(Geostationary Earth Orbit,GEO)卫星,其中MEO卫星分布在三个轨道面。由于北斗三号POD已经可以取得很高的精度,其具备了独立解算地心运动的能力。但目前成熟的光压模型参数均不是针对BDS-3系统提出,各模型对于BDS-3解算地心运动参数究竟会产生怎样的影响,还鲜有深入系统的研究。丰富的轨道面有利于地心运动参数的解算,本实验采用MEO与IGSO卫星进行解算,GEO卫星由于明显的偏差而被排除。
利用BDS-3单系统解算得到的GCC-Z时序以及频谱图如图所示:
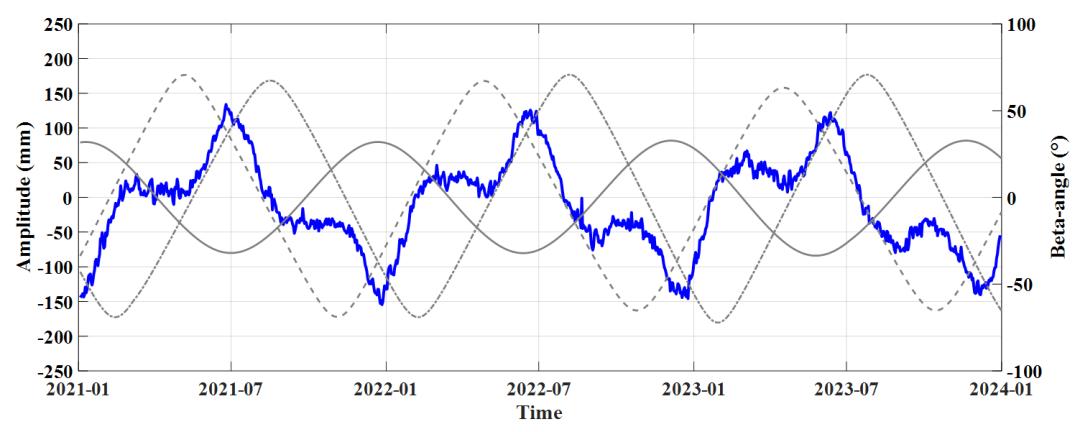
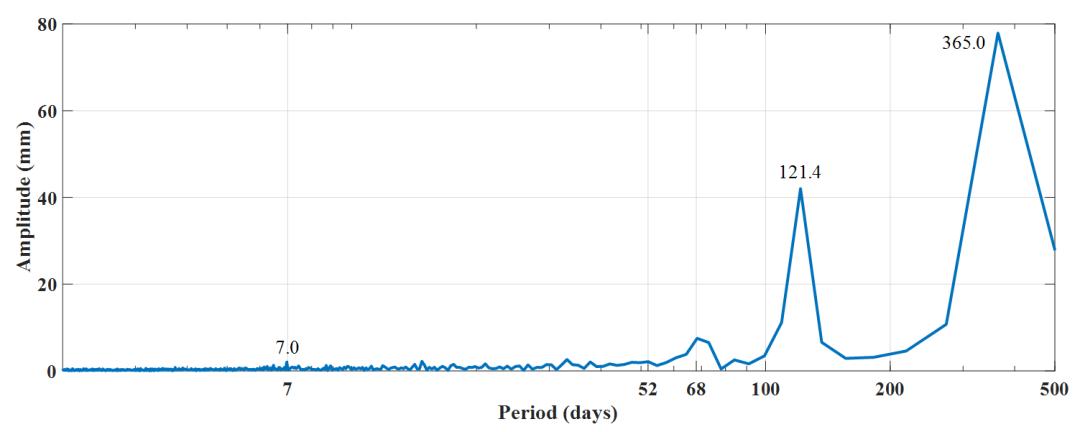
(a)E1求解地心运动Z方向时序与频谱图
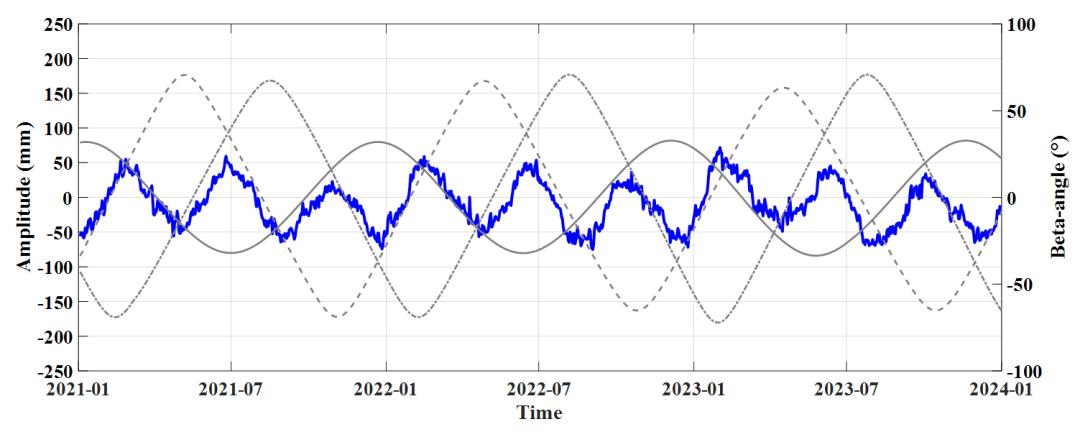
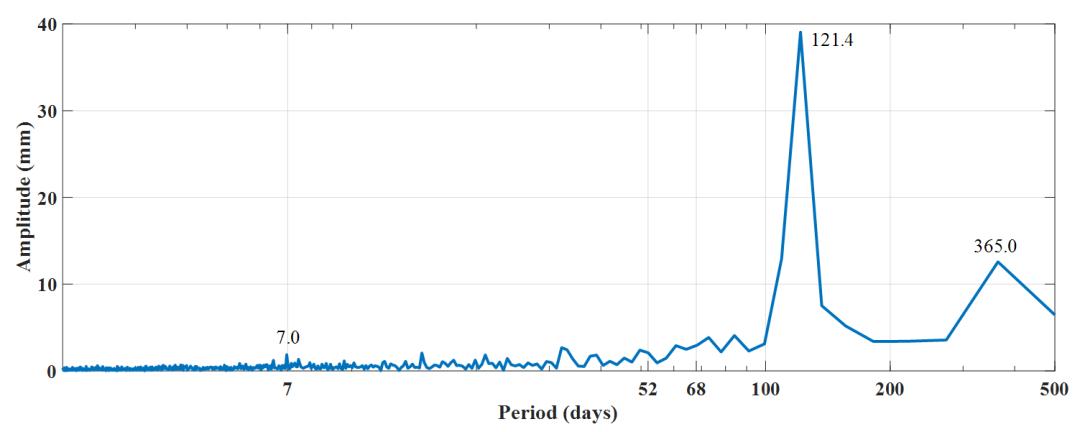
(b)E1+BW求解地心运动Z方向时序与频谱图
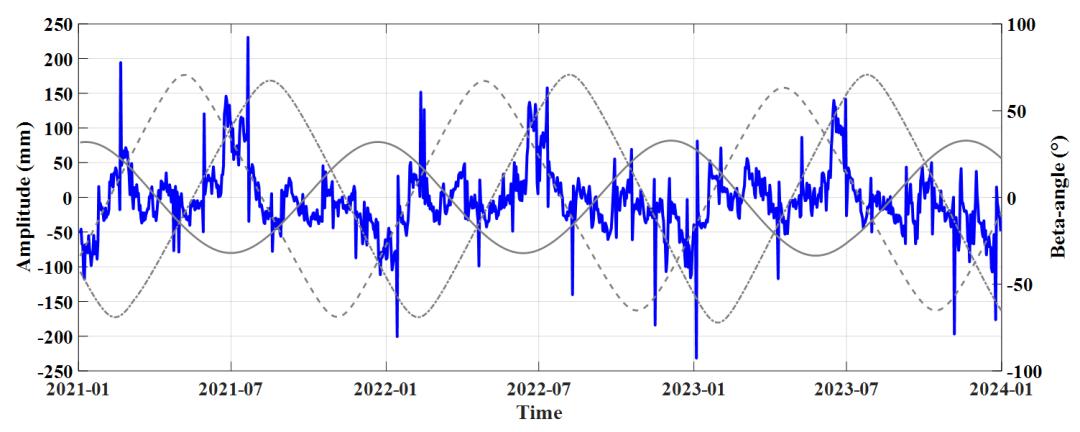
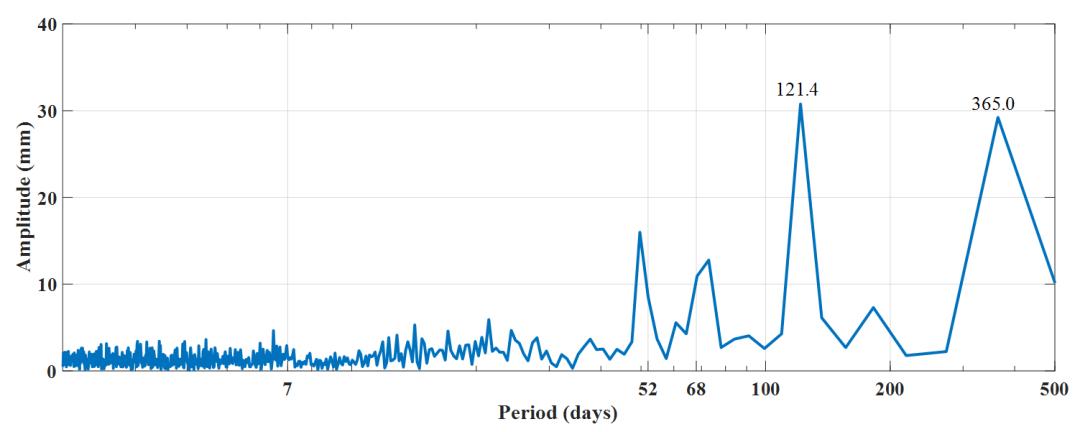
(c)E2求解地心运动Z方向时序与频谱图
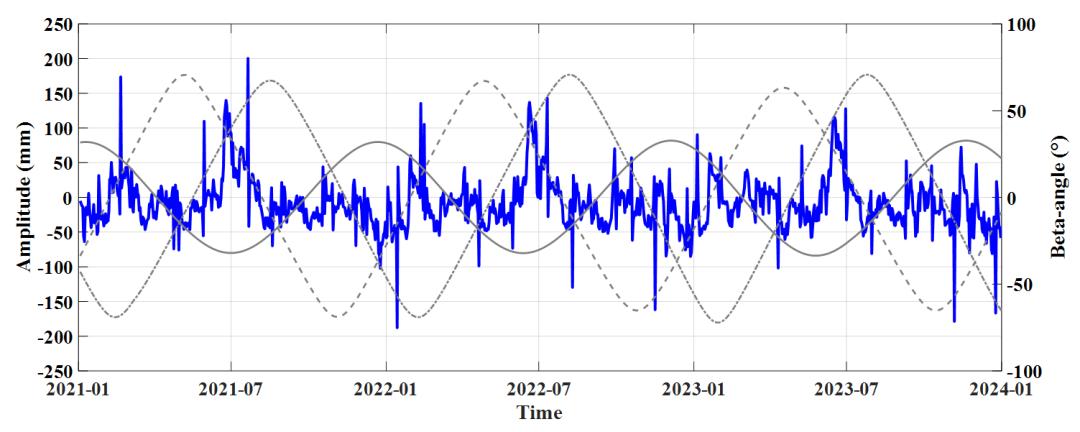
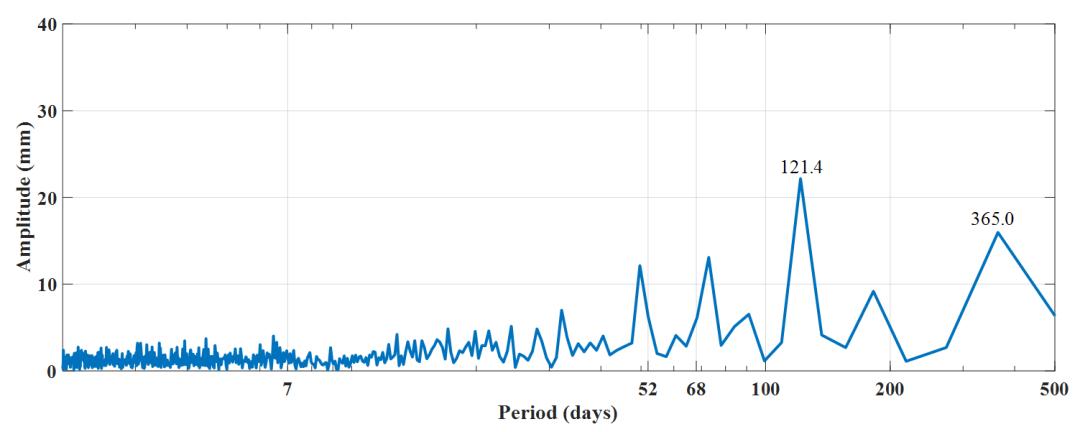
(d)E2+BW求解地心运动Z方向时序与频谱图
图2 BDS-3基于不同SRP配置求解地心运动Z方向时序与频谱图(需注意子图a中纵坐标的变化)
由图2可以清晰地看到,在E1与E1+BW模型下,GCC-Z时序随太阳高度角的变化特性规律性更强,在两轨道面太阳高度角相等且另外一轨道面太阳高度角相差较远处附近取得局部极值。E2与E2+BW模型下在太阳高度角为0°附近时GCC-Z时序会产生明显的跳变,原因是ECOM2模型在地影期间存在较大的建模误差,使得这一时期附近地心运动估计准确性降低。在频谱图中看到了类似GPS、Galileo系统的3-cpy信号,这是由于BDS-3的MEO卫星同样分布在多个轨道面上,是由
β角的周期性造成的交点年误差。E1模型下年周期项振幅为77.9 mm,3-cpy振幅为42.0 mm;加入BW模型后,1-cpy振幅降低为12.6 mm,降低了83.83%,3-cpy振幅降低为39.0 mm,并没有显著下降,3-cpy周期项依旧占据了绝对的主导地位。在E2模型下1-cpy振幅为29.3 mm,3-cpy振幅为30.8 mm;E2+BW模型下1-cpy振幅为16.0 mm,3-cpy振幅为22.2 mm。
除此之外我们发现了与BDS-3系统相关性较高的虚假周期。MEO卫星的轨道太阳高度角约每68 day过零一次,所以在各方案下均探测到了68 day附近的周期信号,尤其是E2方案下最为显著。由于MEO卫星的地面重访周期为7 day,我们也在各方案下探查到周期为7 day的虚假信号,可见这是一个系统性和周期性的错误,不过这一虚假周期的振幅并不大,可以忽略不计。
BW模型的加入改善了地心运动参数的估计,E1+BW与E2+BW模型对比来看,纵使E1+BW下1-cpy取得了更小值,但是其中存在过大的3-cpy交点年误差。E2+BW模型下显著改善了3-cpy周期的主导地位,并且值得注意的是,E2+BW方案探测到了较显著的约为182.5 day的半年周期项,振幅为9.2 mm,这与客观事实更为相符。
我们总结了地心运动三个方向的形式误差,发现了不同的结果:
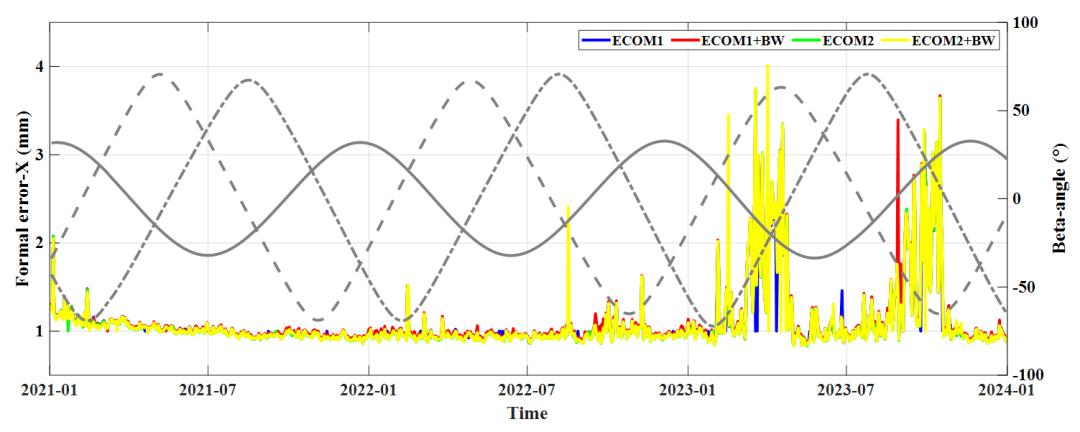
(a)X方向各SRP模型下地心运动参数形式误差
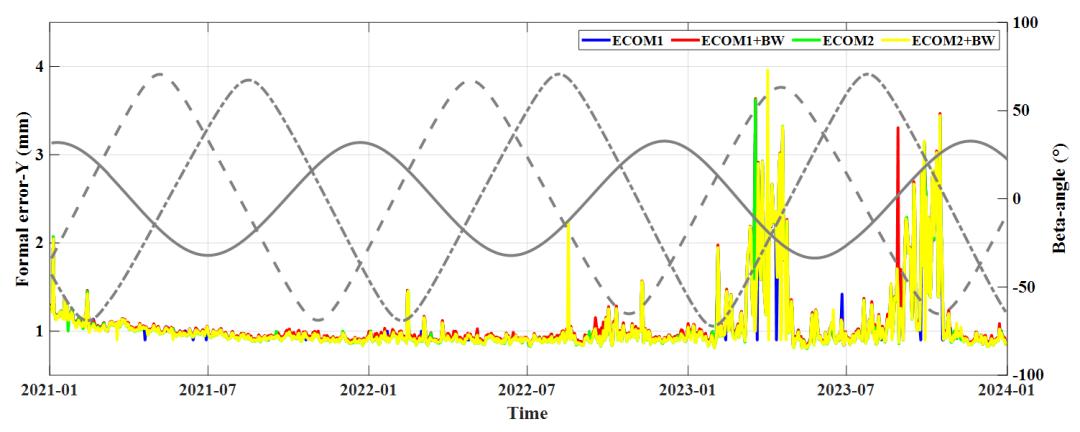
(b)Y方向各SRP模型下地心运动参数形式误差

(c)Z方向各SRP模型下地心运动参数形式误差
图3 BDS-3系统各方向地心运动参数形式误差
BDS-3系统中GCC-X、GCC-Y和GCC-Z中在2023年070~120和250~290两段时间内均产生了形式误差的跳变。抛去这两段时间可以发现GCC-X、GCC-Y形式误差同样几乎不受不同SRP方案选择的影响。GCC-Z中E1与E1+BW方案下形式误差基本平稳,保持在1mm左右波动;E2与E2+BW方案下形式误差呈现出随高度角变化的规律波动性,局部极大值存在一个主波峰和两个次波峰。当三个轨道面
|β|值基本相等时,会产生一个局部主波峰;当两个轨道面
|β|相等且小于第三个轨道面
|β|时会产生一个局部次波峰。轨道面太阳高度角的变化体现出了某一时刻下卫星的空间构型,可见卫星空间构型与地影期间姿态校正情况会对地心运动的解算可靠性产生影响。
为进一步说明不同解决方案对于GCC-Z以及轨道解算的影响,我们统计了不同解决方案下BDS-3各卫星轨道与CODE发布产品相比的综合误差以及每日误差:
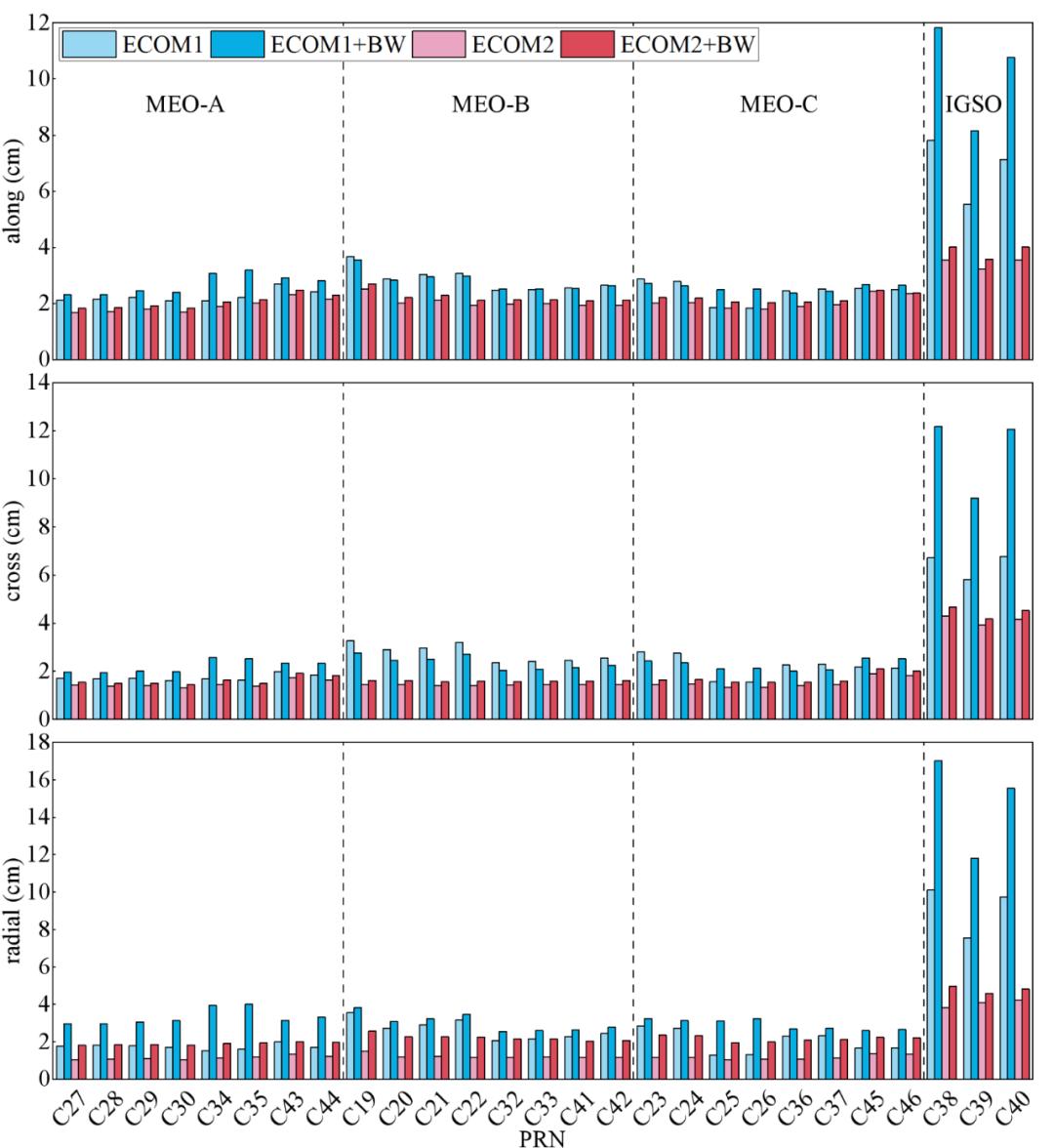
图4 BDS-3的MEO与IGSO卫星在沿轨、跨轨和径向分量上的RMS误差
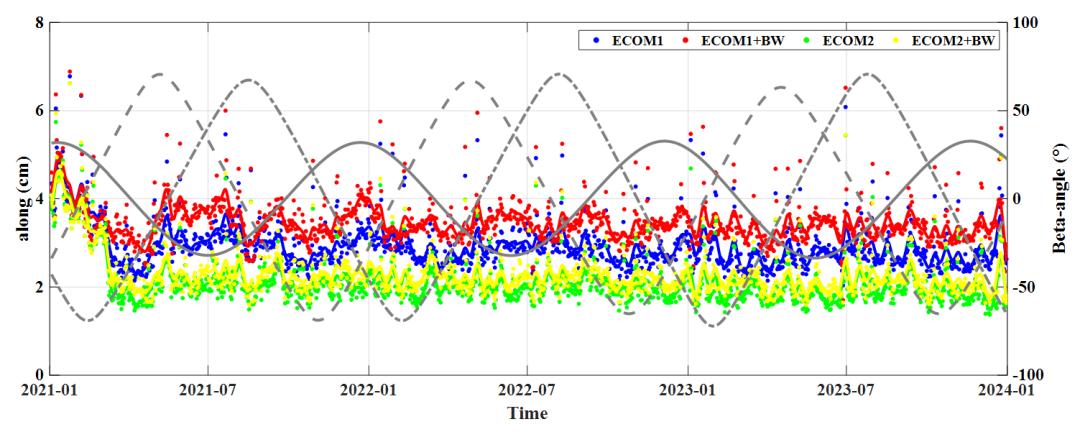
(a)BDS-3的MEO与IGSO卫星在沿轨方向上每日平均轨道RMS
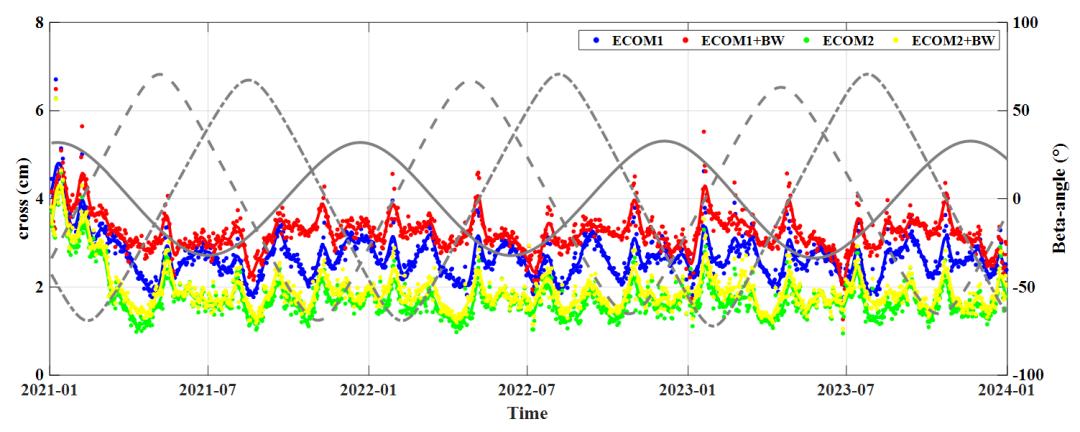
(b)BDS-3的MEO与IGSO卫星在跨轨方向上每日平均轨道RMS
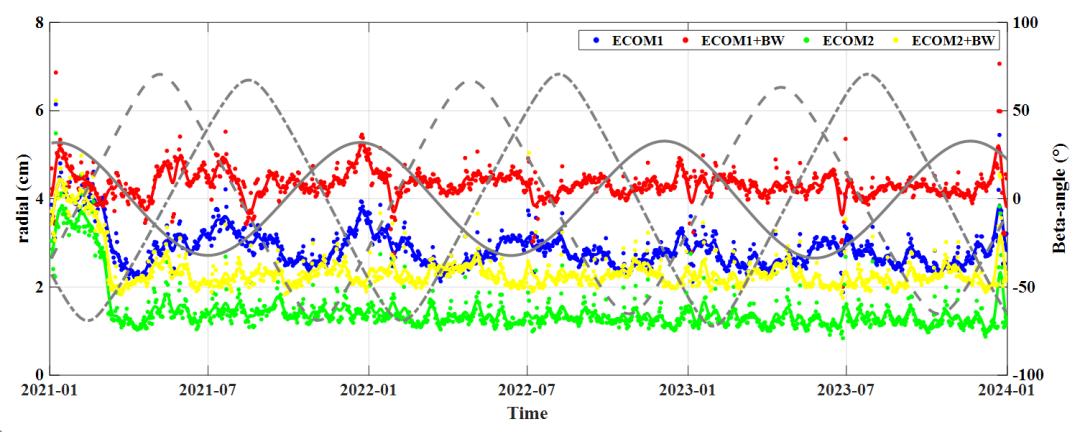
(c)BDS-3的MEO与IGSO卫星在径向方向上每日平均轨道RMS
图5 BDS-3卫星在沿轨、跨轨和径向分量上每日轨道平均RMS统计图
从图中可以清晰的看到,IGSO卫星的轨道精度显然低于MEO卫星,尤其是E1+BW方案下,最大误差达到17.0 cm,这与轨道面特性有关。但更为丰富的轨道面已然被证实会更有利于地心运动的解算,在轨道误差不存在严重错误的情况下,我们依旧保留了三颗IGSO卫星参与地心运动参数的解算。各方案统计指标如表3示:
表3 BDS-3系统采用不同太阳光压模型方案统计指标
单位:cm

在2021年070之前各分量上轨道误差均偏大,这一时期BDS-3观测数据量较少,导致解算结果精度较差。自2021年070开始各解决方案各分量误差均趋于平稳,并无明显错误,说明各类方案均可有效用于BDS-3的POD。我们在各轨道分量上取得了一致的结论,即对于POD而言,精度上方案E2>E2+BW>E1>E1+BW,E2方案相对于E1+BW方案在沿轨、跨轨和径向分量上精度分别提升38.46%、45.68%以及66.67%。
总结
本文基于BDS-3全球导航卫星系统观测数据,系统分析了不同太阳光压模型对BDS-3系统地心运动时序解算及精密定轨的影响,重点探讨了各模型选用的实用性及频谱特性差异。针对BDS-3系统,尽管受限于观测数据稳定性,E2+BW方案仍能有效改善频谱特性,特别是减少了虚假周期信号并探测到半年周期信号,反映出BDS-3解算地心运动参数的可行性。
原标题:《学术交流 | 太阳光压模型对BDS-3地心运动参数解算的影响研究》
