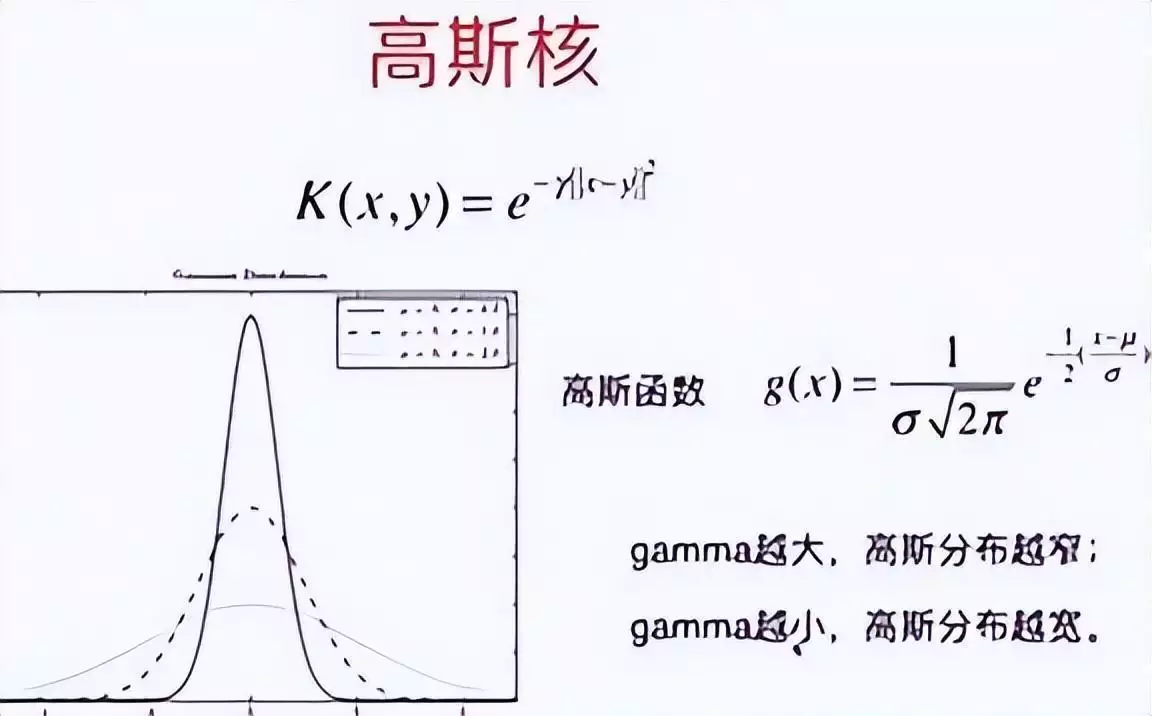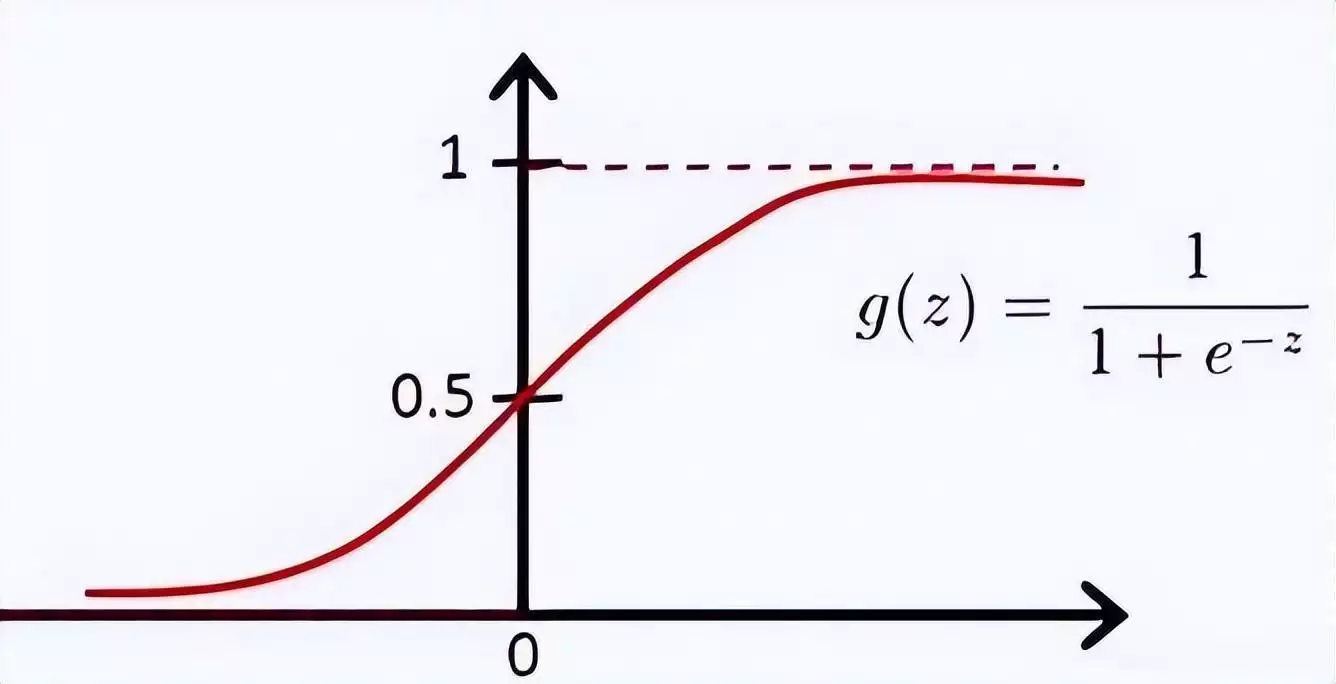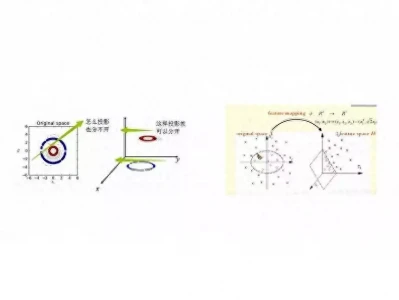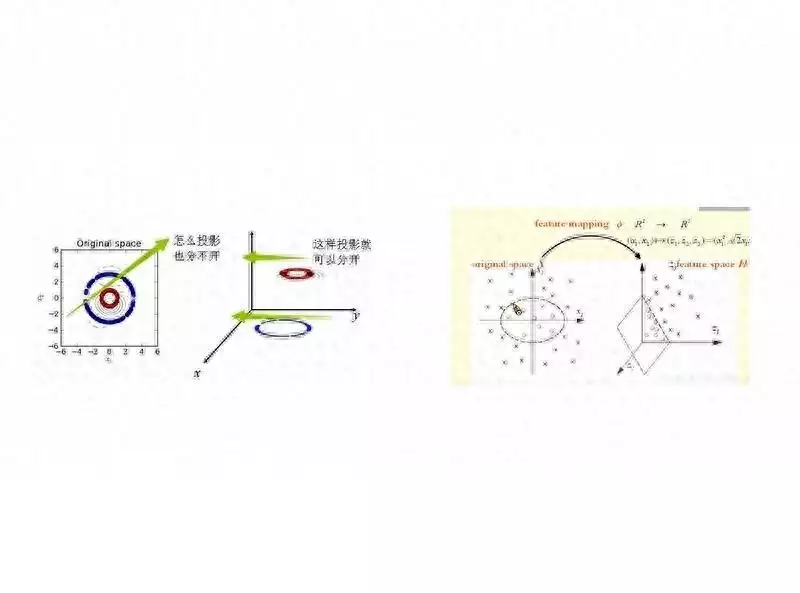
核函数作为一种用于支持向量机的重要数学工具,能够把低维的非线性数据巧妙地映射到高维的线性空间。通过这种映射方式,原本难以区分、不可分的数据就变得可以有效区分了。

核函数发挥作用的原理在于利用内积的性质。它借助一个非线性的变换函数,将数据从原始空间转换到特征空间,随后在特征空间中计算数据的内积,进而得出数据在特征空间中的相似度。
核函数具有诸多优点。一方面,它能够避免直接在高维空间中进行复杂的计算,从而节省了大量的时间和空间开销;另一方面,它还有助于提高分类效果,使得数据分类更加准确和高效。
核函数的常见类型主要有以下几种:
线性核函数:这是最为简单的一种核函数,它直接使用数据的内积,不进行任何额外的变换操作。该核函数适用于线性可分的数据情况,然而对于非线性数据而言,其效果则不尽如人意。 多项式核函数:它是一种基于多项式的核函数类型。这种核函数能够将数据映射到多项式空间,从而增加数据的非线性特征。它可以处理一定程度的非线性数据,不过由于其参数较多,在使用过程中容易出现过拟合的情况。