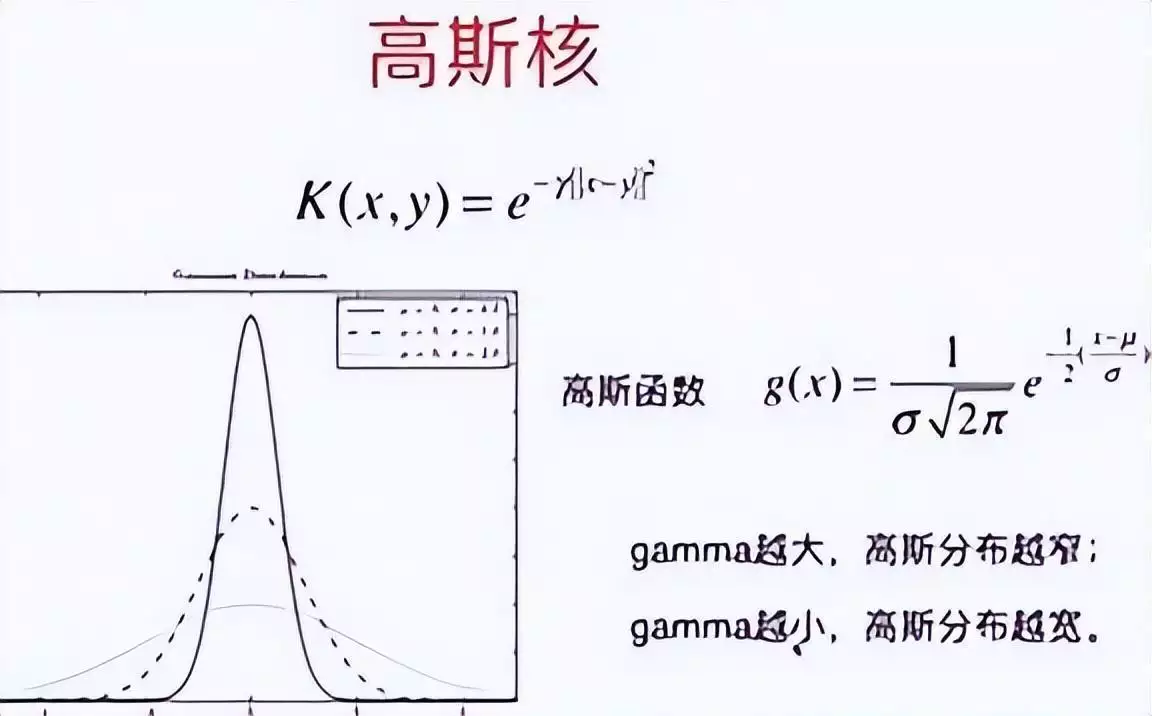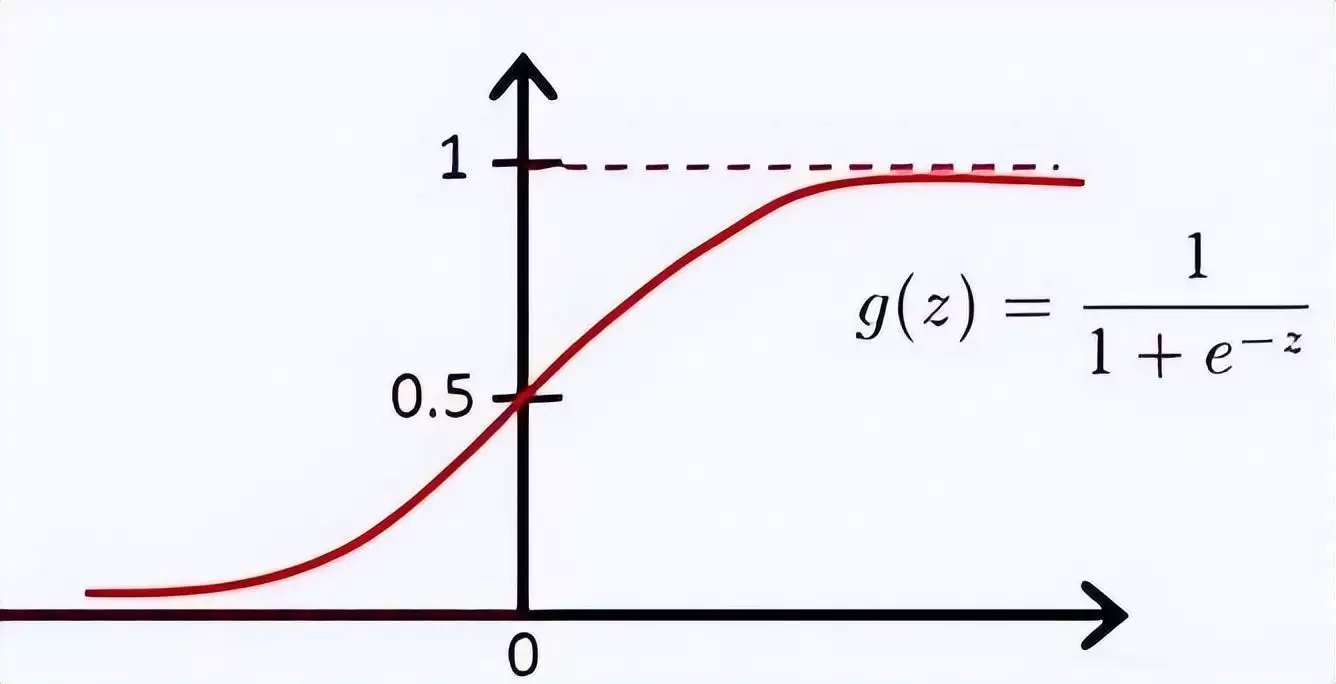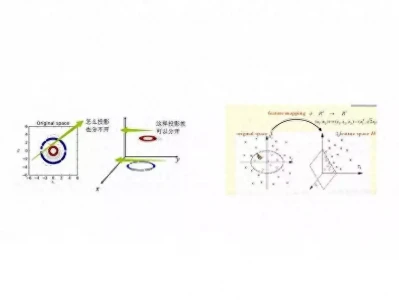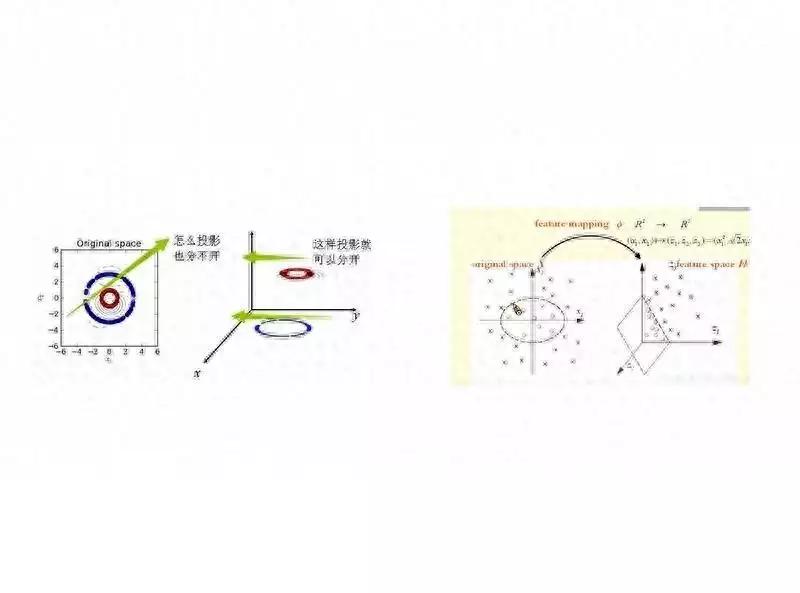
核函数作为支持向量机中的关键数学工具,发挥着重要作用。它能够把低维空间里呈非线性分布的数据,巧妙地映射到高维的线性空间之中。通过这样的转换,原本难以区分、不可分的数据,就变得可以被清晰地划分开来了。

从原理上讲,核函数借助内积的相关性质,利用一个具有非线性特征的变换函数,将数据从原始所处的空间转换到特征空间里。随后,在特征空间中对数据的内积进行计算,以此得到数据在该特征空间中的相似度 。
核函数具有显著的优势,它能避免直接在高维空间中开展复杂的计算工作,这样一来,无论是时间开销还是空间开销都会大幅减少。同时,它还有助于提升分类的效果,让分类结果更加准确可靠。
核函数的常见类型有以下几种:
线性核函数:这是最为简单的一种核函数,它直接采用数据的内积来进行相关操作,不进行任何额外的变换处理。对于线性可分的数据来说,这种核函数比较适用,但要是面对非线性的数据,其效果可能就不太理想了。 多项式核函数:它属于基于多项式的核函数类别,能将数据映射到多项式所构建的空间里,从而为数据增添非线性的特征。该核函数可以应对一定程度的非线性数据,不过由于其参数相对较多,所以在实际应用中比较容易出现过拟合的情况。